Схема замещения асинхронного двигателя

По своей сути, схема замещения АД подобна трансформаторной. Различие состоит лишь в том, что у АД электрическая энергия преобразуется в механическую(а не в электрическую, как в трансформаторе), поэтому на схеме замещения асинхронного двигателя вводят дополнительное активное переменное сопротивление r₂ ‘ , зависящее от скольжения. В трансформаторе, аналогом этого дополнительного сопротивления является сопротивление Z н в нагрузке.

Величина скольжения задается переменным сопротивлением, например, в случае отсутствии нагрузки на валу электродвигателя, скольжение почти нулевое, т.е нулю s≈0, а значит переменное сопротивление стремится к бесконечности, что эквивалентно режиму холостого хода (ХХ). И наоборот, при перегрузке АД, s=1, поэтому сопротивление равно нулю, что эквивалентно режиму короткого замыкания (КЗ).

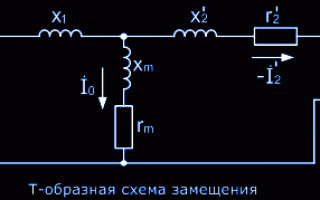
Т-образная схема замещения

Но более удобной и популярной в электротехнике при расчетах считается Г-образная схема замещения АД.

При Г-образном замещении, намагничивающая ветвь выносится к входным зажимам. Т.е, вместо трех ветвей имеем две ветви, одна – намагничивающая, а другая – рабочая. Но данное действие требует внесение поправочного коэффициента c₁, который есть ничто иное как, отношение напряжения подводимого к АД, к ЭДС статора.

Величина c₁≈1, поэтому для максимально возможного упрощения, на практике используют значение c1=1. При этом необходимо учитывать, что c₁ снижается с увеличением мощности АД, поэтому более точное приближение соответствует более мощному электродвигателю.

Для построения векторной диаграммы (ВД) АД требуется чтобы параметры цепи роторной обмотки были приведены к статорной цепи. Этого можно добиться изменением числа витков одно фазной обмотки w₂, с числом фаз m₂ и обмоточным коэффициентом k_об2 на w₁, m₁, k_об1.

Основные электрические параметры должны быть пересчитаны верно, для того чтобы сохранить правильное энергетические соотношения в АД.

ЭДС приведенной вторичной обмотки будет равно:

Вычислив коэффициент трансформации токов, сможем определить приведенный ток вторичной обмотки.

В АД с короткозамкнутым ротором числа фаз m₁ и m₂ не равны, т.к каждый стержень КЗ обмотки рассматривается при расчетах как отдельная фаза, число витков такой обмотки будет равно w₂=0.5, а число фаз будет равно числу стержней m₂=Z₂. Таким образом обмоточный коэффициент для этой обмотки равенk_об2=1. Исходя из этого выражения k_e≠k_i, в отличие от трансформатора.

Активное и индуктивное сопротивления вторичной обмотки АД находится по формулам:

Угол сдвига фаз между E₂’ и I₂’ определяется следующим образом.

Уравнения токов, напряжений, ротора и статора.

На основании уравнений выше можно построить векторную диаграмму АД:

Построение ВД начинается с вектора основного магнитного потока Ф. Затем откладываем вектора E₁ и E₂’ , которые отстают от вектора Ф на угол 90 градусов. Затем зная угол сдвига фаз ψ₂ между током I₂’ и E₂’, можно отложить вектор I₂’. Вектор I будет опережать Ф на угол δ, а вектор I₁ определяют как векторную сумму векторов I и -I₂’. Вектор U₁ построим, добавив к вектору –E₁ падение напряжения I₁r₁ параллельно I₁ вектору, затем откложим jI₁x₁ и получаем вектор I₁Z₁, который сложим с –E₁ и в результате получим U₁.

Т.к АД в этом случае можно рассматривать как трансформатор, работающий на активную нагрузку, то вектор –I₂’r₂’(1-s)/s откладываем под тем же самым углом, что и вектор I₂‘, затем прибавляем к нему –I₂’r₂’ и –jI₂’x₂, получаем в итоге вектор –I₂’Z₂.

42. Схемы замещения асинхронной машины. Т-образные и г-образные схемы замещения

При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентнойсхемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.

По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r₂‘(1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Z_н.

Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.

Как и у трансформатора, у асинхронного двигателя есть Т-образная схема замещения.

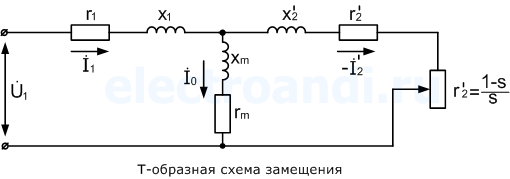
Более удобной при практических расчетах является Г-образная схемазамещения.

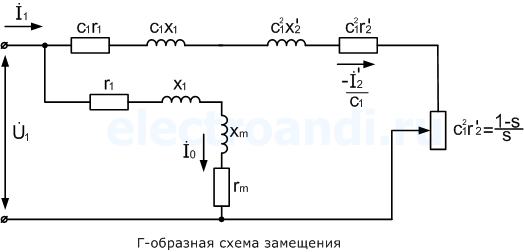
В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c₁, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.

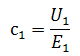
Читать еще: Асинхронный двигатель устройство механическая характеристика

Величина c₁приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c₁≈1. При этом следует учитывать, что значение коэффициента c₁уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.

Параметры схемы замещения рассматриваются подробнее в статье векторная диаграмма асинхронного двигателя

43. Приведение обмотки ротора к обмотке статора.

Для построения векторной диаграммы осуществим приведение параметров обмотки ротора к параметрам обмотки статора. При этом обмотку ротора с числом фаз m₂, обмоточным коэффициентом k₂ и числом витков W₂заменяют обмоткой с соответствующими параметрами статора m₁, k₁, W_1, соблюдая при этом энергетический баланс в роторе.

Методика приведения параметров асинхронного двигателя аналогична методике приведения вторичной обмотки трансформатора. При этом уравнение обмотки ротора (5.4) примет вид

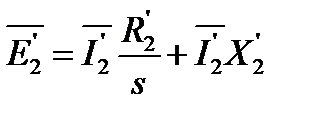
где ;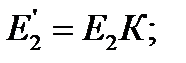

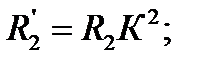
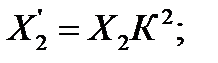
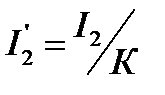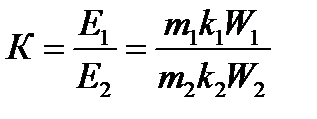
44. Механический момент и механическая мощность ад

Как уже говорилось, взаимодействие тока I₂ в обмотке ротора с потоком асинхронной машины Ф создает механическую силу, приводящую ротор во вращение. При определении вращающего момента, создаваемого этой силой, необходимо исходить из известного физического соотношения, согласно которому мощность, затрачиваемая на приведение тела во вращение, определяется произведением приложенного к нему момента на скорость вращения данного тела.

Как было указано в § 3, на ротор двигателя через вращающийся магнитный поток Ф передается некоторая электромагнитная мощность, рассчитываемая по формуле (33). Однако не вся мощность, переносимая на ротор магнитным потоком, расходуется на приведение его во вращение, поскольку часть ее тратится на нагревание проводников обмотки ротора.

Механическая мощность двигателя, равная разности электромагнитной мощности и мощности потерь [см. формулу (34)], будет равна произведению вращающего момента на частоту вращения ротора:

Р_мех = Мп/9,55, (39)

где М — момент, Н∙м; n — частота вращения, об/мин.

Частота вращения ротора может быть связана с частотой вращения магнитного поля машины, если вспомнить формулу (9), из которой следует:

Во многих случаях для понимания сущности явлений, происходящих в асинхронной машине, полезно иметь в виду еще одно выражение для вращающего момента. Выше мы уже упоминали, что механическая сила, действующая на проводники ротора, создается в результате взаимодействия тока в проводниках обмотки ротора с магнитным полем. Момент асинхронного двигателя можно рассчитать, зная значение приведенного тока в роторе и потока машины

М = c_мI₂Ф_макс cos ψ₂, (43)

где ψ₂ — угол сдвига между э. д. с. Е’₂, наводимой в роторе и током ротора I’₂; c_м — постоянный коэффициент; Ф_макс — магнитный поток, Вб; I’₂ — ток ротора, А.

В области малых скольжений асинхронной машины справедливой является приближенная формула

поскольку cos ψ₂ при малых скольжениях близок к единице

СХЕМА ЗАМЕЩЕНИЯ ФАЗЫ АСИНХРОННОГО ДВИГАТЕЛЯ

Для расчетов рабочих процессов асинхронного двигателя часто используется схема замещения фазы двигателя, состоящая из резистивных и индуктивных элементов с постоянными параметрами, а также резистивного элемента с переменным сопротивлением, замещающим механическую нагрузку на валу двигателя.

Для обоснования такой схемы замещения преобразуем соответствующим образом основные уравнения состояния двигателя. Для этого все роторные величины приведем к числу витков, обмоточному коэффициенту и числу фаз статора подобно тому, как мы приводили к числу витков первичной обмотки трансформатора величины, относящиеся ко вторичной обмотке (см. § 8.5). Асинхронный двигатель является трехфазным устройством, но его фазы симметричны, поэтому достаточно составить схему замещения для одной фазы.

Электродвижущая сила фазы статора Е₁ связана с ЭДС фазы неподвижного эквивалентного ротора Е_2н соотношением

где k_e — коэффициент трансформации напряжений асинхронной машины.

Согласно векторной диаграмме фазы двигателя (рис. 14.18)

— _2н =( +j 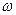L_рас2) ₂ = (r_В2 + r₂ +j 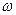L_pac₂) ₂ = Z_o₆₂ ₂ + г₂ ₂.

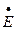— ₁ = (Z_o₆₂ + r₂)k_e ₂.

Ток фазы ротора ₂ можно заменить приведенным током:

₂= (Зw₁k_об1/m₂w₂k_об2) ’₂ = k_i ’₂

где k_i — коэффициент трансформации токов асинхронной машины. Сделав подстановку, получим:

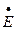₁= — (Z_o₆ ₂ + r₂) k_ek_i ’₂.

Произведение k_ek_i = k есть коэффициент трансформации асинхронной машины.

Введем теперь в уравнения электрического состояния фазы статора асинхронного двигателя приведенные сопротивления цепи ротора:

Элементы с такими сопротивлениями в цепи фазы статора будут потреблять такую же энергию и при том же сдвиге фаз между током и напряжением, как это имеет место в соответствующих сопротивлениях элементов цепи фазы ротора по схеме на рис. 14.17.

Таким образом, ЭДС фазы статора равна:

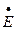₁ = — (Z’_об2 + r’₂) ’₂

а напряжение статора (фазное)

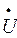₁ = (- 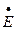₁ ) + Z_o61 ₁ = Z_o61 ₁ + (Z_o62 + r’₂) ’₂. (14.18)

Читать еще: Что такое моментальный двигатель

С другой стороны, ЭДС 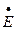₁ пропорциональна намагничивающему току ₁_x и по тем же соображениям, как и для трансформатора, напряжение

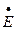(— ₁) = Z₁₂ ₁_x,

где условная величина Z₁₂, модуль которой имеет размерность сопротивления, в эквивалентной схеме замещения соответствует магнитной цепи двигателя. Следовательно, для напряжения фазы статора справедливо также второе уравнение

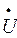₁ = Z_0б1 ₁+ Z₁₂ _1х. (14.19)

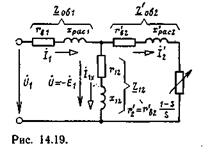
Вместе с уравнением тока статора

₁ = _1х + ’₂ (14.20)

два уравнения напряжения фазы статора (14.18) и (14.19) можно рассматривать как уравнения, соответствующие законам Кирхгофа для цепи на рис. 14.19. В ней элементы Z_o₆₁ изображают схему замещения обмотки фазы статора, Z’_q_б2 — обмотки фазы ротора, Z₁₂ — магнитную цепь машины, a r’₂ — механическую нагрузку.

Уточним, что ток _1х является током фазы статора идеального холостого хода двигателя, т. е. это ток двигателя в условиях, когда ток в роторе отсутствует (I₂ = 0). Ток 1₁_x можно измерить, если посредством внешнего двигателя довести ротор до синхронной частоты вращения (s = 0).

При такой синхронной частоте вращения сопротивление резистивного элемента, соответствующего механической нагрузке в эквивалентной схеме замещения, равно (14.16):

r’₂ = r’_B2/s — r’_B2 = r’_B2 (1 — s)/s = .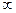

Если затормозить двигатель до полной остановки, то s = 1 и, следовательно,

По этой причине опыт полной остановки двигателя именуется опытом короткого замыкания — обычно он осуществляется при сильно пониженном напряжении на статоре.

4. Расчет схемы замещения

Упрощенная эквивалентная схема замещения двигателя постоянного тока приведена на рисунке 4.1

Рисунок 4.1 Схема замещения двигателя

Определим номинальную скорость вращения якоря исходя из каталожного значения частоты вращения

Активное сопротивление якорной обмотки:

где для двигателей постоянного тока независимого возбуждения;

для двигателей постоянного тока смешанного возбуждения.

для двигателей постоянного тока последовательного возбуждения.

Индуктивность обмотки якоря определяется в соответствии с формулой Уманского:

где k = 0.2 — 0.25 для компенсированных машин;

k = 0.5 — 0.6 для некомпенсированных машин.

Принимаем k = 0.25

Момент инерции для машины постоянного тока составляет

Номинальный коэффициент потока

Таблица 4.1 Параметры двигателя

ДПУ 240 1100 3 Д4109

Номинальная частота вращения якоря

Активное сопротивление якорной обмотки

Индуктивность обмотки якоря

Делись добром 😉

1. Преимущества и недостатки системы ШИП — ДПТ
1.1 Импульсные преобразователи постоянного напряжения (общие сведения)
1.2 Анализ существующих импульсных преобразователей
2. Функциональная схема лабораторного стенда
3. Разработка технической документации на лабораторный стенд системы ШИП — ДПТ
3.1 Общий вид лабораторного стенда
3.2 Принципиальная схема стенда после доработки
3.3 Перечень функциональных возможностей лабораторного стенда
3.4 Система управления на базе микроконтроллера PIC 16F 877
4. Расчет схемы замещения
5. Статические характеристики системы ШИП — ДПТ
6. Выбор силовых элементов
6.1 Выбор силового трансформатора
6.2 Выбор силового транзистора
6.3 Выбор обратного диода
7. Расчет преобразователя
8. Расчет энергетических характеристик
9. Математическая модель системы ШИП — ДПТ

ЭЛЕКТРОМЕХАНИКА

Научно-технический журнал

Редколлегия
Авторам
Архив
Подписка
Редакционная этика журнала
Контакты
English version

Известия высших учебных заведений. ЭЛЕКТРОМЕХАНИКА 2016; 6: 13-17

Определение параметров схемы замещения асинхронного двигателя с короткозамкнутым ротором по справочным данным

В.И. Котенев, А.В. Котенев, В.В. Кочетков

Котенев Виктор Иванович – д-р техн. наук, профессор кафедры «Электроснабжение промышленных предприятий» Самарского государственного технического университета.

Котенев Александр Викторович – канд. техн. наук, доцент кафедры «Электроснабжение промышленных предприятий» Самарского государственного технического университета. E-mail: [email protected]

Кочетков Владимир Валерьевич – аспирант кафедры «Электроснабжение промышленных предприятий» Самарского государственного технического университета. E-mail: [email protected]

Разработана методика вычисления сопротивлений асинхронного двигателя с короткозамкнутым ротором по каталожным данным. Номинальные сопротивления определены из решения трех уравнений, два из которых получены из уравнения электромагнитной мощности при номинальном и критическом скольжении, а третье – из уравнения реактивной мощности рассеяния при номинальном скольжении. Зависимости активного сопротивления роторной обмотки и индуктивного сопротивления двигателя от скольжения приняты традиционными, в которых значения этих сопротивлений в режиме короткого замыкания получены из решения уравнений пускового тока и электромагнитной мощности при скольжении, равном единице. Индуктивное сопротивление намагничивающей ветви получено из уравнения реактивной мощности этой ветви.

Ключевые слова: асинхронный двигатель, короткозамкнутый ротор, схема замещения, параметры, расчет, паспортные данные

Ссылки на литературу

1. Кравчик А.Э. и др. Асинхронные двигатели серии 4А: справочник. М.: Энергоатомиздат, 1982.

2. Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей. М.: Энергоатомиздат, 1984.

3. Иванов-Смоленский А.В. Электрические машины. М.: Изд. дом МЭИ, 1980. 3-е изд. Т. 1, 2006. 652 с.

4. Костенко М.П., Пиотровский Л.М. Электрические машины. В 2-х частях. Ч. 2. Машины переменного тока. Л.: Энергия, 1973.

5. Осипов В.С., Котенев В.И., Кочетков В.В. Определение параметров схем замещения асинхронных двигателей с фазным и короткозамкнутым ротором // Вестн. Сам. гос. техн. ун-та. Сер. Техн. науки. 2013. №3(39). С. 175 – 184.

6. Мощинский Ю.А., Беспалов В.Я., Кирякин А.А. Определение параметров схемы замещения асинхронной машины по каталожным данным // Электричество. 1998. № 4. C. 38 – 42.

7. Гридин В.М. Расчет параметров схемы замещения асинхронных двигателей по каталожным данным // Электричество. 2012. № 5. C. 40 – 44.

8. Качин С.И., Чернышев А.Ю., Качин О.С. Автоматизированный электропривод: учеб.-метод. пособие. Томск: Изд-во Томского политехн. ун-та, 2010. 162 с.

9. Котенев А.В., Котенев В.И., Кочетков В.В. Определение сопротивлений короткозамкнутого асинхронного двигателя по каталожным данным // Вестн. Сам. гос. техн. ун-та. Сер. Техн. науки. 2016. № 1(49). С. 103 – 109.

10. Сивокобыленко В.Ф., Ткаченко С.А., Деркачев С.В. Определение параметров схем замещения и характеристик асинхронных двигателей // Электричество. 2014. № 10. C. 38 – 44.

11. Boglietty A., Cavagino A., Ferrari L. Induction motor equivalent circuit including the stray load losses in the machine power balance // IEEE Transaction on Energy Conversion. 2008. Vol. 23. Iss. 3. P. 796 – 803.

Схема замещения асинхронного двигателя