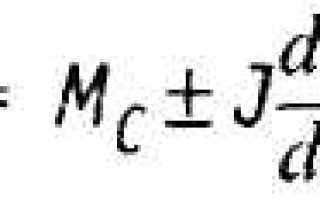Элементы механики электропривода

Уравнение движения ЭП

где М — вращающий момент двигателя, Н*м,

Мс – приведенный к валу двигателя момент сопротивления РН, Н*м

J – приведенный к валу двигателя момент инерции ЭП, Н*м2

ω — угловая частота вращения двигателя, рад /с.

Величина называется динамическим или избыточным моментом ЭП. Положительный динамический момент обеспечивает разгон ЭП, отрицательный — замедление.

Мощность двигателя, Вт,

Поскольку (где n измеряется в об/мин),

Номинальный момент двигателя можно вычислить по приводимым в паспорте номинальной мощности Рн и номинальной скорости вращения двигателя nн:

Приведенный к валу двигателя момент сопротивления, Н*м,

где j и η — соответственно передаточное отношение и КПД передачи,

Приведенный к валу двигателя момент инерции ЭП, в котором сочетаются вращательное и поступательное движения (например, ЭП лифта):

где: Jд — моменты инерции ротора двигателя, Н*м2

JРM — момент рабочего механизма, Н*м2,

ωрм — частота вращения рабочего механизма, рад /с;

G — вес перемещаемого посредством ЭП груза, кг;

v — линейная скорость перемещения груза, м/с,

g — ускорение силы тяжести, 9,8 м/с2.

Определение времени ускорения и замедления ЭП

Время t1-2 ускорения или замедления ЭП от частоты вращения ω1 до ω2 определяется путем интегрирования уравнения движения ЭП:

В простейшем случае, когда М = const, Мс = const, J= const, no лучим

В частном случае, при пуске двигателя до частоты вращения со, время пуска U с, определяется выражением:

После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.

2.14 Масса двигателя и динамический момент инерции ротора

Масса изолированных проводов обмотки статора:

Масса алюминия короткозамкнутого ротора с литой клеткой (число лопаток на роторе N=14, ширина лопатки средняя b_л=5мм, длина лопатки l_л=70мм, высота h_л=56мм):

Масса стали сердечников статора и ротора:

Масса изоляции статора:

Масса конструкционных материалов:

Динамический момент инерции:

Делись добром 😉

АННОТАЦИЯ
ВВЕДЕНИЕ
1. АНАЛИТИЧЕСКИЙ ОБЗОР
1.1 Современные серии электрических машин
2. Расчеты и основные результаты работы
2.1 Техническое задание
2.2 Выбор аналога двигателя
2.3 Размеры, конфигурация, материал магнитной цепи двигателя
2.4 Обмотка статора
2.5 Обмотка короткозамкнутого ротора
2.6 Расчет магнитной цепи.
2.7 Активные и индуктивные сопротивления обмоток
2.8 Режим холостого хода и номинальный
2.9 Рабочие характеристики.
2.10 Максимальный момент.
2.11 Начальный пусковой момент и пусковые токи
2.12 Расчет механической характеристики двигателя и зависимости пускового тока от скольжения
2.13 Тепловой и вентиляционный расчеты
2.14 Масса двигателя и динамический момент инерции ротора
2.15 Расчет надежности обмотки статора
2.16 Механический расчет вала и подбор подшипников качения.
ЗАКЛЮЧЕНИЕ

Идентификация момента инерции якоря двигателя постоянного тока и нагрузки в экспериментальной вибрационной установке для исследования хаотической динамики

Полный текст:

Аннотация
Об авторах
Список литературы
Cited By

Аннотация

Цель исследования. Статья посвящена разработке и апробации методики оценки параметров моментов инерции якоря двигателя постоянного тока с независимым возбуждением (ДПТ НВ) и его нагрузки, используемых в лабораторной вибрационной установке для исследования хаотической динамики.

Методы. Представлена математическая модель ДПТ НВ и описание методики для оценки величины момента инерции его якоря с нагрузкой в результате параметрической идентификации на основе аппроксимации проинтегрированной кривой разгона силы тока и выполнения спектрального анализа. Проведено совместное моделирование динамики электродвигателя Maxon RE25 с электрической частью, реализованной в системе Matlab Simulink и механической, построенной в среде MSC Adams, и на основе результатов машинного эксперимента проверена работоспособность методики параметрической идентификации.

Результаты. Представлена структура и общий вид информационно-измерительной системы лабораторной вибрационной установки для исследования хаотической динамики на основе модуля ввода/вывода NI USB-6009. Приведены и проанализированы кривые разгона и амплитудные спектры силы тока, полученные в ходе проведения натурного эксперимента по определению моментов инерции якоря двигателя Maxon RE25 и дебалансов. Произведен расчет значений моментов инерции якоря и дебаланса по предлагаемой методике, а также относительных погрешностей по сравнению с паспортным значением.

Заключение. В результате проведения серии параллельных экспериментов установлено, что опыты являются воспроизводимыми согласно критерию Кохрена, а погрешность определения момента инерции якоря ДПТ не превышает 5 %, поэтому ее можно также использовать для расчетов с достаточной точностью величин моментов инерции дебалансов.

Ключевые слова

Об авторах

Дмитрий Александрович Бушуев, кандидат технических наук, доцент кафедры технической кибернетики

Список литературы

1. Zhusubaliyev Z.T., Avrutin V., Rubanov V.G., Bushuev D.A., Titov D. V., Yanochkina O.V. Persistence border collisions in a vibrating system excited by an unbalanced motor with a relay control // AIP Conference Proceedings. 2018. Vol.1959. №080022.

2. Salah M. S., Abdelati M. Parameters Identification of a Permanent Magnet DC Motor Conference // IASTED International Conference on Modelling, Identification and Control (MIC 2010), Austria (February 2010), 2010.

3. Гаргаев А.Н., Каширских В.Г. Идентификация параметров двигателей постоянного тока с помощью поисковых методов // Вестник Кузбасского государственного технического университета. 2013. С. 131-134

4. Krneta R., Antic S., Stojanovic D. Recursive least square method in parameters identification of DC motors models // Facta Universitatis. 2005. 18 (3). P. 467–478.

5. Hadef M., Bourouina A.. Mekideche M. R. Parameter identification of a DC motor via moments method // International Journal of Electrical and Power Engineering. 2008. 1(2). P. 210–214.

6. Гаргаев А.Н., Каширских В.Г., Нестеровский А.В. Сравнительный анализ методов динамической идентификации параметров электродвигателей // Сб. трудов XI международной научно-практической конференции «Безопасность жизнедеятельности предприятий в промышленно развитых регионах» (24-25 ноября 2015 г.). Кемерово: КГТУ им. Т.Ф. Горбачева, 2015.

7. Wu W. DC Motor Parameter Identification Using Speed Step Responses // Modelling and Simulation in Engineering. 2012. №189757.

8. Tutunji T. A. DC motor identification using impulse response data // Conference on EUROCON, Serbia & Montenegro (22-24 November 2005). 2005. P. 1734-1736

9. Lord W., Hwang J. H. Pasek’s Technique for Determining the Parameters of HighPerformance DC Motors // Proceedings of the Third Annual Symposium on Incremental Motion Control Systems and Devices. University of Illinois. May 1974. P. R.1-10,

10. Hadef M., Mekideche M.R. Moments and Pasek’s methods for parameter identification of a DC motor // Journal of Zhejiang University – Science C. 2011. 12(2). P. 124-131.

11. Волков Н.И., Миловзоров В.П. Электромашинные устройства автоматики. 2-е изд., перераб. и доп. М., 1986. 335 с.

12. Patent EP0193761B1, 03.04. 1998. Strunk T. L., Westerman G.S. Method for testing DC motors. 29.05.1991.

13. Бушуев Д.А., Рубанов В.Г., Бажанов А.Г. Методы интеграции моделей электродвигателей в среду MSC.Adams для совместного моделирования динамики механи ческих объектов с системами управления // Сб. докл. междунар. науч.-техн. конф. БГТУ им. В. Г. Шухова «Наукоемкие технологии и инновации». Белгород: БГТУ им. В.Г. Шухова, 2016. С. 10-14.

Для цитирования:

Рубанов В.Г., Бушуев Д.А., Паращук Е.М., Трикула А.K. Идентификация момента инерции якоря двигателя постоянного тока и нагрузки в экспериментальной вибрационной установке для исследования хаотической динамики. Известия Юго-Западного государственного университета. 2019;23(2):97-108. https://doi.org/10.21869/2223-1560-2019-23-2-97-108

For citation:

Rubanov V.G., Bushuev D.A., Parashchuk E.M., Trikula A.K. Identification of Anchor Inertia Motor Moment of Direct Current and Loading in Experimental Vibration Installation for Chaotic Dynamics Study. Proceedings of the Southwest State University. 2019;23(2):97-108. (In Russ.) https://doi.org/10.21869/2223-1560-2019-23-2-97-108

Контент доступен под лицензией Creative Commons Attribution 4.0 License.

Что такое момент инерции двигателя

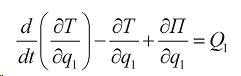
где T-кинетическая энергия агрегата;

Q — обобщенная сила;

П — потенциальная энергия системы ;

i= 1.2.3. К -число степеней свободы системы.

Уравнение лагранжа представляет совокупность дифференциальных уравнений с K oобобщенными координатами по числу степеней свободы. Для изучения тяговой динамики агрегата при установившемся движении агрегата будем иметь одно уравнение.

Перемещение и скорость агрегата можно задать угловой скоростью коленчатого вала и связанную с ней поступательной скоростью агрегата

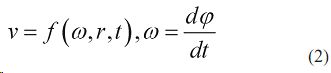
Произведение обобщенной силы на обобщенную координату определяет работу системы. За обобщенную силу Q примем разность — крутящего момента , и момента сопротивления движению агрегата от крюковой и дополнительной тяговой нагрузки,приведенных к валу двигателя

Читать еще: Шевроле лачетти двигатель какой тип

определяет касательную силу тяги трактора; -силу тяги на крюке и другие силы сопротивления движению

Кинетическая энергия мобильного агрегата равна

I_a — момент инерции агрегата, приведенный к валу двигателя упругая связь трактора с комбинированной машиной определяется уравнением потенциальной энергии пружины

где с — коэффициент жесткости упругой связи трактора с комбинированной мащиной

x — величина продольной деформации упругой связи машины с трактором (навески, амортизатора,пружины,тяговых соединений и т.д.)

С учетом полученных уравнений (2–5), общее уравнение динамики для тракторного агрегата имеет вид:

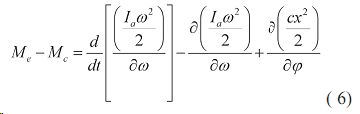
Для представления уравнения (6) в развернутом виде и его решения необходимо знать функциональные зависимости входящих в это уравнение величин. Величина приведенного момента инерции зависит от скорости движения агрегата. В свою очередь на величину скорости влияют буксование движителей — δ, деформация упругой связи — δ_y, буксование муфты сцепления — δ_m, потери жидкости в гидростатической передаче — δ_r.

Каждый из этих коэффициентов определяется отношением скоростей

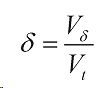
V_t — рассчетная скорость агрегата;

V_δ — действительная скорость агрегата.

С учетом всех коэффициентов снижения скорости, действительная скорость движения определяется зависимостью

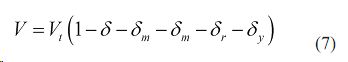
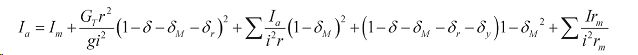
Приведенный момент инерции будет равен

I_m-момент инерции маховика и приведенных к нему масс двигателя;

i — передаточное число трансмиссии трактора ;

G_T — полный вес трактора;

I_r — момент инерции любой вращающейся детали;

i_rM -передаточное число от вала двигателя к любой детали I_rM -момент инерции любой вращающейся детали при вращении от вала отбора мощности;

i_r — число от двигателя к любой детали;

G_a = G_m + G_Т полный вес комбинированного агрегата.

r_к — радиус ведущих колес трактора;

G_m — полный вес комбинированной ма- шины.

При выключенной муфте сцепления или полном буксовании δ_m=1, а все члены уравнения ( 8) равны нулю .Тогда I_a=I_m .

Для тракторов с механической трансмиссией δ_r=0

После трогания комбинированного агрегата влияние упругих деформаций связей незначительно, поэтому разность можно заменить — определяющей к.п.д. учитывающего потери на буксование мобильного агрегата. Тогда приведенный момент инерции будет равен:

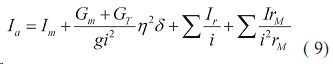
Ограничимся анализом влияния на приведенный момент инерции и на динамику трактора двух наиболее важных факторов — переменного передаточного отношения трансмиссии и к.п.д. буксования, включая в это понятие учет потерь скорости под действием факторов ,определяемых уравнением (7).При указанных условиях уравнение (6) приводится к виду:

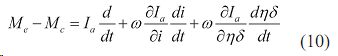
При постоянных передаточных числах трансмиссии и буксовании, уравнение упрощается

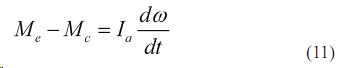
Задача максимального динамического нагружения на механизмы трансмиссии решалась В.Н. Болтинским. Для оценки влияния трансмиссии и буксования на снижение динамических нагрузок найдем частные производные уравнения (9) и сделаем преобразования:

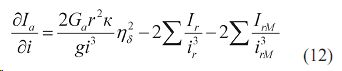
Производную передаточного числа трансмиссии заменим равенством:

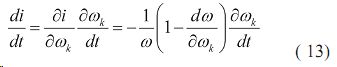
Для последнего члена правой части уравнения (10) справедливо:

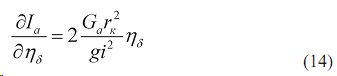
При η_δ=1-δ dη_δ=-dδ в пределах линейной зависимости буксования от силы тяги на крюке справедливо равенство δ=mP_кр и d_δ=mdP_кр, где m — постоянный коэффициент интенсивности буксования. С учетом записи

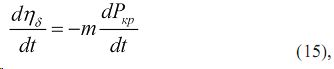
уравнения (10) и зависимостей (12,12,13,14, 15) получим :

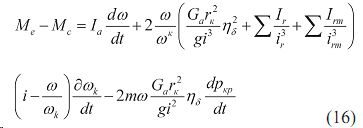
Для трактора со ступенчатой трансмиссией ω/ ωk=1 средний член равенства (16) обращается в нуль, а уравнение имеет вид:

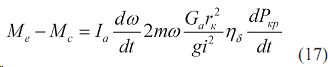
При непрозрачной трансмиссии =0 остаточный крутящий момент равен:

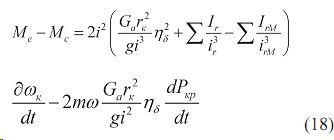
С увеличением скорости движения при уменьшении передаточного числа и при наличии бесступенчатой трансмиссии снижаются динамические нагрузки. При увеличении приведенного момента инерции повышается устойчивость и равномерность движения агрегата ,поскольку растет обобщенная сила системы.

Приведенный момент инерции существенно влияет как на колебания комбинированного агрегата относительно линии тяги трактора, так и на агротехнические погрешности, возникающие при отклонениях от прямолинейного хода рабочих органов.

Исходя из уравнения лагранжа применительно к перемещению комбинированной машины в параметрах динамической схемы нагружения, получим конечные уравнения, описывающие поведение динамической системы

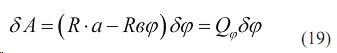
Приравнивая значения обобщенной силы, имеем:

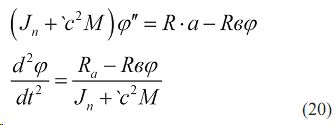
Это дифференциальное уравнение является математической моделью движения комбинированного агрегата.

Где а — расстояние от центра давления до главной оси инерции агрегата ;

в — расстояние от равнодействующей центра давления до центра тяжести агрегата;

´с – плечо момента устойчивости (от центра тяжести до точки прицепа агрегата).

Разделим правую часть на коэффициент при, и сделав замены :

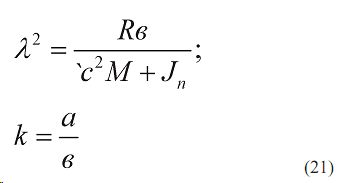
Получим дифференциальное уравнение колебаний комбинированного агрегата относительно точки прицепа:

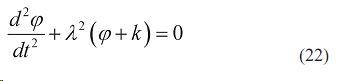
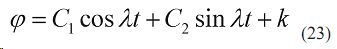
Произвольные постоянные C1,C2 определяют:

При t=0, φ=0, φ´=0, C1=–k,C2=0

Опуская промежуточные вычисления, уравнение можно привести к виду:

Заменяя k и λ их значениями, получим геометрические и динамические соотношения параметров комбинированного агрегата.

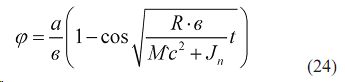
Амплитуда колебаний от внешних сил и изменения параметров системы смещается в сторону увеличения угла φ. Уравнение (24) показывает, что с увеличением асимметрии внешней нагрузки и с увеличением смещения от оси вращения, угол φ возрастает. С другой стороны при увеличении c´ угол φ уменьшается. При увеличении веса и момента инерции рыхлителя, колебания системы становятся более плавными, а их амплитуда уменьшается обратно пропорционально корню квадратному из величин роста момента инерции устройства. При проектировании рабочего органа необходимо уменьшать k, увеличивая значения в.

Для стабилизации плавности хода агрегата необходимо увеличивать его продольный размер .

Смещение центра тяжести равно

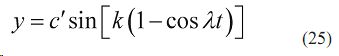
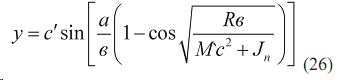
Уравнение (26) можно представить в виде одночлена удобного для операционных вычислений по уравнению

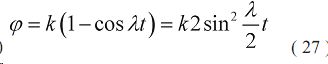
Для этого значения подставляем в уравнение :

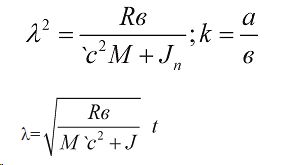
В итоге получим закономерность влияния только момента инерции агрегата на изменения угла λ отклонения от положения равновесия. Для этого примем значение k

Установлено, что при увеличении ширины захвата возрастает момент инерции агрегата .При этом одновременно стабилизируется плавность хода и возрастает его производительность.

Читать еще: Renault sandero какой двигатель выбрать

Заключение

Полученные уравнения тяговой динамики в дифференциальной форме позволяют выявить и оценить факторы, влияющие на динамическую напряженность трактора и комбинированной машины. При увеличении момента инерции агрегата уменьшаются его угловые и линейные колебания , а динамическая система при этом работает более устойчиво.

Экспериментальное определение моментов инерции ротора или якоря электрической машины

Не всегда значение маховых моментов или моментов инерции роторов или якорей электрических машин можно найти в каталогах электрооборудования. Также в данный момент на предприятиях эксплуатируется большое количество электрических машин, данные на которые могут потеряться в ходе эксплуатации. Если данные о маховом моменте электрической машины отсутствуют, то их можно определить экспериментально с помощью методов:

Крутильных колебаний;
Маятниковых колебаний;
Падающего груза;
Свободного выбега;

Метод крутильных колебаний

Суть данной методики заключается в следующем: ротор электромашины подвешивают на стальной проволоке за конец вала. Второй конец проволоки жестко закрепляют на опоре, как показано на рисунке ниже (а):

При таком определении момента инерции нужно строго обеспечить вертикальность оси вала ротора. После чего ротор, подвешенный на проволоке, закручивают на определенный угол и подсчитывают количество полных колебаний z, которые ротор совершит за какой – то промежуток времени t. Период полного колебания, если пренебречь затуханием, можно представить:

Где k – направляющий момент проволоки (момент, вызывающий закручивание проволоки на 1 радиан). Если мы знаем k, то момент инерции ротора можно определить из следующего выражения:

k можно определить исходя из размеров проволоки:

Где Е – модуль кручения для материала проволоки в кГ/см 2 ;

r и l – радиус и длина проволоки в см соответственно.

Так как формула не дает точного значения k, более точно можно определить его из опыта. Для этого нужно измерять вращающий момент М, необходимый для закручивания проволоки на угол α. Тогда:

Но еще проще произвести определение момента инерции на основе двух опытов крутильных колебаний ротора. Для этого измеряют продолжительность полного колебания как указано выше. Второе измерение периода колебания ротора производят с прикрепленным к нему телом, момент инерции которого известен J_доб. Как вариант, это может быть диск с известными геометрическими размерами и весом или рычаг с грузами на концах (рис. выше б). если Т – период колебаний одного ротора, а Т / — с добавочным грузом, тогда получим выражение:

Благодаря пропорциональности между углом отклонения и направляющим моментом угол первоначального закручивания может быть взят произвольным.

Метод маятниковых колебаний

Ротор машины крепят проволокой к куску угловой стали так, чтоб вершину уголка можно было использовать в качестве призмы, относительно которой ротор электромашины смог бы выполнять колебания. После чего оба конца полученного таким образом маятника опирают на металлические горизонтальные опоры так, чтоб ротор мог относительно точек опоры совершать колебания. Момент его инерции относительно оси, совпадающей с вершиной уголка, при пренебрежении инерцией последнего будет равен:

Где: G – это вес ротора машины в кг;

е – расстояние между осью ротора и осью качания, измеряется в м;

Т – период одного колебания в сек.

Зная J_N, определяют по общему правилу инерцию ротора относительно оси, проходящей через центр тяжести:

Метод падающего груза

Самым главным недостатком методик, описанных выше, является то, что для определения инерции необходима разборка электромашины. Метод падающего груза позволит определить момент инерции электродвигателя без разборки последнего.

На конец вала или шкив, сидящий на валу, навивают несколько витков шнура. К другому концу шнура прикрепляют груз и опускают его через направляющие блоки, либо непосредственно, как показано ниже:

При опускании груз поворачивает ротор, преодолевая трение в подшипниках электромашины, при этом измеряют время t, за которое груз опустится на величину h.

В таком случае инерция ротора может быть вычислена по формуле:

Где: m – масса груза

r – радиус вала или шкива, на который навивается шнур;

t и h – время, и соответственно высота опускания груза;

g – ускорение свободного падения равное 9,81;

Метод свободного выбега

Перечисленные выше методы определения инерции электрической машины больше подходят к электрическим машинам относительно малой мощности. При значительных габаритных и массовых показателей машин большой мощности определение инерции методами маятниковых колебаний и падающего груза становятся практически не пригодными, и тем более не пригодны в системе электродвигатель – рабочий орган. Поэтому зачастую применяют метод свободного выбега.

Когда двигатель отключают от сети, то за счет накопленной кинетической энергии, двигатель и соединенный с ним рабочий орган будет вращаться замедляясь постепенно. Чем больше тормозящее усилие сил трения и чем меньше запас кинетической энергии, тем быстрее будет замедлятся система. Имея кривую самоторможения, показанную ниже, которая представляет собой график зависимости скорости от времени.

По данной кривой можно сделать вывод о величине тормозных усилий. Мощность торможения в данном случае будет равна уменьшению кинетической энергии во времени:

Подставив в формулу значение кинетической энергии , которая представлена в джоулях, тогда получим:

Из данного выражения можно определить момент инерции:

Величину поднормали определяют из кривой торможения для точки, в которой известны потери энергии при торможении. Если масштабы выбраны, то для построения кривой самоторможения: µ_n = об/мин/см – скорость, µ_t = сек/см – времени. В таком случае масштаб поднормали будет равен: , то есть , где СВ выражена в см.

Элементы механики электропривода