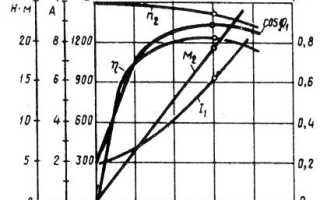
Рабочие характеристики асинхронного двигателя

Рабочие характеристики асинхронного двигателя

Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.

Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 — s).

Скольжение s = Pэ2/Pэм, т. е. скольжение асинхронного двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1.

По мере увеличения нагрузки на валу асинхронного двигателя отношение s = Pэ2/Pэм растет, достигая значений 0,01 — 0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора двигателя r2′ угол наклона этой кривой увеличивается. В этом случае изменения частоты асинхронного двигателя n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2′ возрастают электрические потери в роторе.

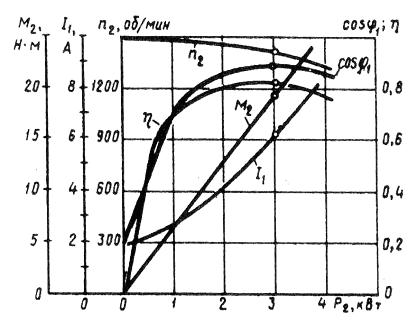
Рис. 1. Рабочие характеристики асинхронного двигателя двигателя

Зависимость М2 =f(P2). Зависимость полезного момента на валу асинхронного двигателя М2 от полезной мощности Р2 определяется выражением M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2,

где Р2 — полезная мощность, Вт; ω2 = 2πf 2/ 60 — угловая частота вращения ротора.

Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.

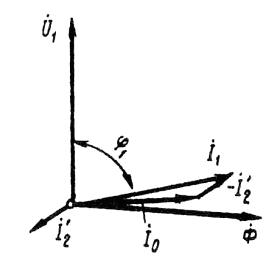
Зависимость cos φ1 = f (P2). В связи с тем что ток статора асинхронного двигателя I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму холостого хода. Объясняется это тем, что ток холостого хода электродвигателя I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора относительно напряжения получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рис. 2).

Коэффициент мощности асинхронных двигателей в режиме холостого хода обычно не превышает 0,2. При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80 — 0,90) при нагрузке, близкой к номинальной. Дальнейшее увеличение нагрузки на валу двигателя сопровождается уменьшением cos φ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе.

В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cos φ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя.

На рис. 3 представлены графики зависимости cos φ1, асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).

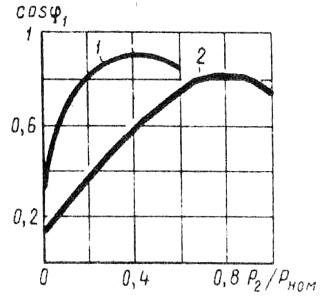
Рис. 3. Зависимость cos φ1,от нагрузки при соединении обмотки статора двигателя звездой (1) и треугольником (2)

Механические характеристики. Энергетические режимы электропривода переменного тока

Для получения механической характеристики ещё более упростим модель — вынесем контур намагничивания на зажимы — рис. 4,а, как это часто делается в курсе электрических машин.

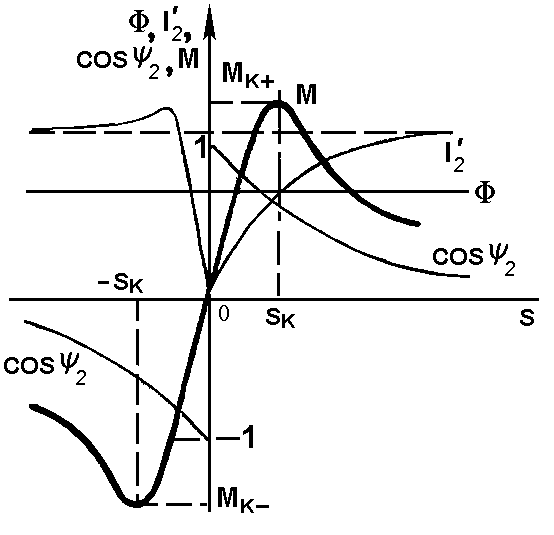
Рис. 4. Упрощенная схема замещения (а) и характеристики асинхронной машины (б)

,

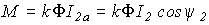где I 2а — активная составляющая тока ротора,

y 2 — угол между 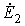и ,

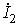качественное представление о механической характеристике М(s) можно получить, проследив зависимость каждого из трех сомножителей от s .

Магнитный поток Ф в первом приближении в соответствии с (4) не зависит от s — рис. 4,б. Ток ротора (8) равен нулю при s = 0 и асимптотически стремится к 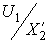при s ® ± Ґ — рис. 4,б. Последний сомножитель легко определить по схеме замещения:

;

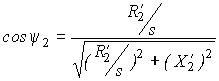cosy 2 близок к ± 1 при малых s и асимптотически стремится к нулю при s ® ± Ґ . Момент, как произведение трех сомножителей, равен нулю при s = 0 (w = w 0 — идеальный холостой ход), достигает положительного М к+ и отрицательного М к- максимумов — критических значений при некоторых критических значениях скольжения 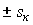, а затем при s ® ± Ґ стремится к нулю за счет третьего сомножителя.

Уравнение механической характеристики получим, приравняв потери в роторной цепи, выраженные через механические и через электрические величины. Мощность, потребляемая из сети, если пренебречь потерями в R 1 , примерно равна электромагнитной мощности:

,

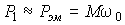а мощность на валу определяется как

.

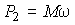Потери в роторной цепи составят

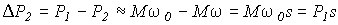(9)

или при выражении их через электрические величины

,

.

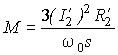Подставив в последнее выражение I 2ў из (8) и найдя экстремум функции М=f(s) и соответствующие ему М к и s к , будем иметь:

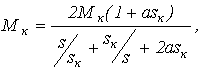(10)

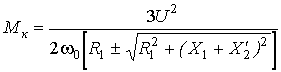; (11)

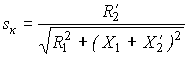. (12)

На практике иногда полагают, что а = 0, т.е. пренебрегают активным сопротивлением обмоток статора. Это обычно не приводит к существенным погрешностям при Р н > 5 кВт, однако может неоправданно ухудшить модель при малых мощностях. При а = 0 выражения (10) — (12) имеют вид:

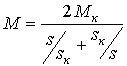; (10,a)

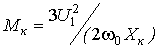; (11,a)

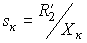, (12,а)

где Х к = Х 1 +Х 2 ’ — индуктивное сопротивление рассеяния машины.

В уравнении (10,а) при s к можно пренебречь первым членом в знаменателе и получить механическую характеристику на рабочем участке в виде

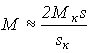. (13)

Как следует из рис. 4,б и выражений (10) и (10,а), жесткость механической характеристики асинхронных двигателей переменна, на рабочем участке , а при Ѕ sЅ > Ѕ s крЅ — положительна.

Асинхронный электропривод как и электропривод постоянного тока, может работать в двигательном и трех тормозных режимах с таким же, как в электроприводе постоянного тока распределением потоков энергии — рис. 5.

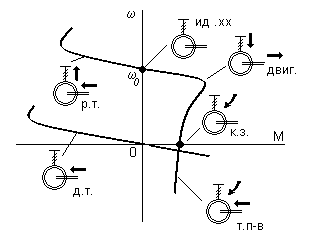
Рис. 5. Энергетические режимы асинхронного электропривода

Рекуперативное торможение (р.т.) осуществляется при вращении двигателя активным моментом со скоростью w > w 0 . Этот же режим будет иметь место, если при вращении ротора со скоростью w уменьшить скорость вращения поля w 0 . Роль активного момента здесь будет выполнять момент инерционных масс вращающегося ротора.

Для осуществления торможения противовключением (т. п-в) необходимо поменять местами две любые фазы статора — рис. 6. При этом меняется направление вращения поля, машина тормозится в режиме противовключения, а затем реверсируется.

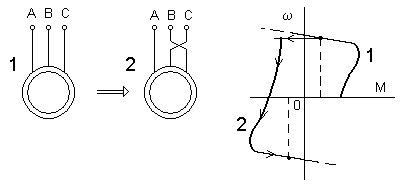
Рис. 6. Реверс асинхронного двигателя

Специфическим является режим динамического торможения, которое представляет собою генераторный режим отключенного от сети переменного тока асинхронного двигателя, к статору которого подведен постоянный ток I п . Этот режим применяется в ряде случаев, когда после отключения двигателя от сети требуется его быстрая остановка без реверса.

Постоянный ток, подводимый к обмотке статора, образует неподвижное в пространстве поле. При вращении ротора в его обмотке наводится переменная ЭДС, под действием которой протекает переменный ток. Этот ток создает также неподвижное поле.

Складываясь, поля статора и ротора образуют результирующее поле, в результате взаимодействия с которым тока ротора возникает тормозной момент. Энергия, поступающая с вала двигателя, рассеивается при этом в сопротивлениях роторной цепи.

В режиме динамического торможения поле статора неподвижно скольжение записывается как

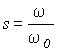
и справедливы соотношения для механической характеристики аналогичные (10,а) — (12,а):

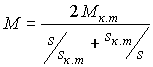, (14)

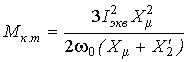, (15)

где 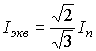при соединении обмоток статора в звезду

и 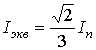при соединении обмоток статора в треугольник;

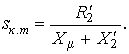(16)

Так как при ненасыщенной машине 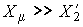, критическое скольжение в режиме динамического торможения s к.т существенно меньше s к .

Специальные регулируемые асинхронные двигатели

Специальные регулируемые асинхронные двигатели создаются в результате адаптации общепромышленных асинхронных двигателей к их условиям эксплуатации в управляемых электроприводах, имеющие в итоге более высокие энергетические и массогабаритностоимостные показатели по сравнению с неадаптированными.

Работа асинхронного двигателя в регулируемом электроприводе (ЭП) характеризуется существенными особенностями, которые и определяют предъявляемые к ним специфические технические требования. Эти особенности связаны с изменяющимися в заданных пределах, а часто и по заданным законам, значениями частот вращения двигателя, величин и частот питающего двигатель напряжения или тока, наличием и необходимостью учёта временных высших гармонических составляющих. В силу этого специфическими являются математические модели (ММ) электромагнитных, электромеханических, энергетических, тепловентиляционных процессов в установившихся и переходных режимах работы двигателей, расчетов добавочных магнитных потерь, механических и виброакустических показателей, которые построены на усовершенствованных расчетных методиках.

Использование серийных асинхронных двигателей (АД) в электроприводах с полупроводниковыми преобразователями (ПП) не оптимально по массогабаритным, энергетическим и другим показателям. По некоторым оценкам использование обычных серийных АД в частотном приводе снижает КПД и требует завышения их установленной мощности на 15-20 % при работе в установившихся режимах и до 40-45 % при работе в динамических режимах. Из-за высших гармоник напряжения и тока на выходе преобразователя частоты на 5-6 % возрастают потери в двигателе.

Необходимо проектирование специальных регулируемых асинхронных двигателей (РАД) с улучшенными регулировочными, динамическими и виброакустическими свойствами. Применение РАД, спроектированных с учётом специфики их работы в условиях регулируемого ЭП, вместо общепромышленных АД дает возможность значительно снизить массу, габариты и стоимость электроприводов, улучшить их функциональные показатели. Если оптимально спроектировать двигатель для частотного регулирования, можно получить на 25 % большую мощность, чем у общепромышленных АД того же габарита, либо уменьшить объем при той же мощности.

Содержание

• 1 Технические предпосылки
• 2 Принципы и методология проектирования
• 3 Особенности и требования
• 4 Адаптация
• 5 Ссылки

Технические предпосылки [ править | править код ]

Техническими предпосылками, обеспечивающими преимущества адаптированных регулируемых двигателей над серийными машинами, являются:

• Исключение требований к пусковым характеристикам (не ставится задача обеспечения кратностей пускового и максимального моментов), в связи с чем может быть применена соответствующая форма паза ротора (отказ от глубоких пазов), обеспечивающая минимальное активное сопротивление обмотки ротора и меньшую индуктивность рассеяния;
• требуемую частоту вращения производственного механизма, определяемую частотой питания двигателя, числом полюсов обмотки статора АД и передаточным числом редуктора, можно обеспечить при различных сочетаниях этих трех величин;
• возможность некоторого снижения перегрузочной способности АД, поскольку система привода отслеживает параметры напряжения или тока питания двигателя;
• использование эффективных систем само- и, при необходимости, принудительного охлаждения;
• возможность выбора оптимального соотношения нестандартных значений напряжения и частоты проектируемого двигателя, отличного от базового и согласованного с номинальными значениями преобразователя, что позволяет снизить массу и габариты;
• усиление электроизоляции витков обмотки статора с целью защиты от импульсных перенапряжений;
• использование соответствующих подшипников с учётом, как высоких скоростей вращения, так и появления паразитных токов от высокочастотной коммутации.

Принципы и методология проектирования [ править | править код ]

Основные принципы и методология проектирования РАД должны базироваться на системном подходе и определяться с учётом существенной специфики их работы в составе ЭП как в установившихся, так и в динамических режимах. Системный подход предусматривает рассмотрение РАД во взаимодействии с другими элементами ЭП: силовой преобразовательной частью, системой управления и регулирования, исполнительным органом рабочей машины. Эффективность системного подхода при проектировании РАД основывается на учёте особенностей отдельных составляющих ЭП, характера отношений и связей между этими составляющими. Благодаря этому значительно повышаются адекватность ММ и соответственно качество проектного синтеза РАД. Использование системного подхода позволяет реализовывать комплексный анализ проектируемого РАД, на основе которого рассматриваются все наиболее важные для проектного синтеза аспекты устройства и функционирования РАД.

Системный подход дает возможность осуществить:

• комплексный учёт всей необходимой совокупности проектных факторов в их взаимосвязи и взаимовлиянии;
• разработку и применение адекватных ММ, учитывающих изменение параметров во всем диапазоне регулирования, и другие особенности работы РАД в регулируемом ЭП;
• обоснование и применение рациональной декомпозиции проектной ММ и модели объекта проектирования, процессов проектного синтеза и оптимизации;
• реализацию эффективных методов оптимизации;
• системную организацию технологии процесса проектного синтеза РАД.

Исходя из системного подхода, определяются специфические проектные критерии и ограничения, используемые при проектировании РАД.

Проектные ММ на основе принципа декомпозиции могут быть составлены с использованием моделей отдельных компонентов ЭП, в том числе и модели объекта проектирования — РАД. Модель РАД должна учитывать полигармонический состав питающего напряжения переменных величины и частоты, изменение параметров двигателя в процессе регулирования и ряд других проектных особенностей. Полупроводниковые преобразователи, отличающиеся типами, силовыми схемами, видами регулирования, законами управления и т. д., представляются разными ММ. Нагрузки ЭП имеют различные законы изменений моментов сопротивлений от частоты вращения и различные уровни. Они могут быть непрерывного или циклического действия. Все это должно найти отражение в ММ нагрузок. Работа АД в системах с ПП обладает существенной спецификой, которая является причиной появления новых требований к параметрам и технико-экономическим показателям РАД, в результате чего задача разработки машин для указанных систем переросла в самостоятельную проблему, включающую и круг вопросов, связанных с определением оптимальных параметров двигателей. Для решения задач проектного синтеза и оптимизации таких двигателей не могут быть применены стандартные методы и программное обеспечение, разработанные для АД общепромышленного назначения.

Особенности и требования [ править | править код ]

При проектировании РАД учитываются следующие особенности и требования:

• необходимость использования в системе расчетного проектирования комплексных ММ, включающих в себя модели всех взаимодействующих компонентов ЭП, а не только модели двигателя, как это делается при проектировании общепромышленных АД;
• выполнение проектирования на определенный диапазон частот вращения, что требует проведения большого объема поисковых и поверочных расчетов;
• формирование набора специфичных критериев оптимальности.

При проектировании РАД для приводов с ПП, как и при выборе серийных АД для этих приводов, могут использоваться также такие критерии как масса, габариты, стоимость двигателя или диапазонные критерии — энергетические показатели двигателя и приведенные затраты. Особые диапазонные критерии оптимальности обуславливают специфику их определения. В частности, энергетические показатели — КПД и коэффициент мощности, приведенные затраты должны рассматриваться в виде эквивалентных усредненных значений для всего диапазона регулирования. При необходимости в состав критериев включаются аналогичные критерии приводов в целом. В ряде случаев может применяться обобщенный критерий, представляющий собой скалярную свертку вышеуказанных критериев с различными коэффициентами их значимости. В установившихся режимах специфика работы РАД заключается, прежде всего, в том, что в каждой рабочей точке двигатель питается определенным по качественно-количественному составу полигармоническим напряжением, зависящим от типа, вида регулирования, закона управления преобразователя, и работает в общем случае с определенным нагрузочным моментом. В разных рабочих точках диапазона регулирования значения параметров схем замещения двигателя различны. Они определяются с учётом вытеснения токов в обмотках и насыщения магнитной цепи машины. Эти особенности положены в основу оптимизационно-поисковых расчетов.

Адаптация [ править | править код ]

Задача адаптации электромашинной части регулируемых ЭП к специфическим условиям работы решается как задача структурно-параметрической оптимизации РАД. Трудоемкость задачи проектирования обусловлена не только необходимостью формирования множества рациональных структур РАД, но и необходимостью решения задачи параметрической оптимизации для каждой сформированной структуры. По своей направленности задачи структурного синтеза можно разделить на внутренние (относящиеся к АД) и внешние (относящиеся к системе привода). Задачей параметрической оптимизации является определение такого набора значений управляемых переменных некоторой сформированной структуры электропривода и входящего в него РАД, при котором целевая функция имеет наилучшее значение. При этом выполняются все требования и ограничения, оговоренные в задании на проектирование. Множество структур РАД с оптимизированными параметрами является информационным базисом для выбора оптимального варианта РАД.

Системный подход предусматривает рассмотрение всех аспектов функционирования РАД. Поэтому при проектном синтезе РАД используется ряд подсистем, с помощью которых осуществляются поверочные расчеты. К их числу относятся расчеты механических и виброакустических показателей, неустановившихся режимов работы. Проектные ММ подсистем так же, как и модели оптимизационно-поисковых расчетов, являются комплексными, составленными из ММ входящих в привод элементов, и в них выполнен учёт рассмотренной выше специфики. При наличии в техническом задании на проектирование РАД активных ограничений, прямо не связанных с электромагнитными, электромеханическими, тепловыми процессами, задача условной оптимизации решается на основе сочетания методов уступок по критериям и релаксации ограничений.

Использование информационных технологий автоматизированного проектного синтеза, прикладного математического и программного обеспечения позволяет реализовать следующие варианты:

• проектирование и производство серий РАД на основе тщательного анализа рынка потребления;
• разработка РАД для использования в регулируемых ЭП конкретных электромеханических систем;
• редизайн АД, использующегося в настоящее время в определенных регулируемых ЭП с целью их адаптации к специфическим условиям работы.

УСТАНОВИВШИЕСЯ РЕЖИМЫ И СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТРЕХФАЗНОГО АСИНХРОННОГО ДВИГАТЕЛЯ ПРИ ПИТАНИИ ОТ ОДНОФАЗНОЙ СЕТИ

Полный текст:

• Аннотация
• Об авторах
• Список литературы
• Cited By

Аннотация

Разработана математическая модель для исследования работы трехфазного асинхронного двигателя с короткозамкнутым ротором при питании обмотки статора от однофазной сети. Для создания вращающегося магнитного поля одна из фаз питается через конденсатор. Вследствие несимметрии не только переходные процессы, но и установившиеся режимы являются динамическими, поэтому в любой системе координат описываются дифференциальными уравнениями. Их исследование не может быть с достаточной адекватностью осуществлено на основе известных схем замещения и требует использования динамических параметров. В математической модели уравнения состояния контуров статора и ротора составлены в неподвижной трехфазной системе координат. Расчет установившегося режима выполняется путем решения краевой задачи, что дает возможность получить зависимости координат на периоде, не прибегая к расчету переходного процесса. Для этого исходные нелинейные дифференциальные уравнения алгебраизируются путем аппроксимации переменных кубическими сплайнами. Полученная нелинейная система алгебраических уравнений является дискретным аналогом исходной системы дифференциальных уравнений. Ее решение выполняется методом продолжения по параметру. Для расчета статических характеристик как функции некоторой переменной данная система дифференцируется аналитически, а затем интегрируется численным методом по этой переменной. В процессе интегрирования на каждом шаге или через несколько шагов производится уточнение методом Ньютона, что дает возможность осуществить интегрирование методом Эйлера за несколько шагов. Матрицы Якоби в обоих случаях совпадают. Для учета вытеснения тока в стержнях короткозамкнутого ротора каждый стержень вместе с короткозамыкающими кольцами разбивается по высоте на несколько элементов. В результате на роторе получаем несколько короткозамкнутых обмоток, эквивалентирующихся трехфазными обмотками, между которыми существуют магнитные связи.

Ключевые слова

Об авторах

Адрес для переписки: Маляр Василий Сафронович – Национальный университет «Львовская политехника», ул. С. Бандеры, 12, 79013, г. Львов, Украина Тел: +38 032 258-21-19 E-mail: [email protected]

Список литературы

1. Брускин, Д. Э. Электрические машины и микромашины / Д. Э. Брускин, А. Е. Зорохович, В. С. Хвостов. М.: Высш. шк., 1990. 528 с.

2. Вольдек, А. И. Электрические машины / А. И. Вольдек. Л.: Энергия, 1978. 832 с.

3. Меркин, Г. Б. Конденсаторные электродвигатели для промышленности и транспорта / Г. Б. Меркин. М.-Л.: Энергия, 1966. 223 с.

4. Тазов, Г. В. Математическая модель асимметричной асинхронной машины / Г. В. Тазов, В. В. Хрущев // Электричество. 1989. № 1. С. 41–49.

5. Торопцев, Н. Д. Трехфазный асинхронный двигатель в схеме однофазного включения с конденсатором / Н. Д. Торопцев. М.: Энергоатомиздат, 1988. 95 с.

6. Мощинский, Ю. А. Математическая модель асинхронного конденсаторного двигателя по методу симметричных составляющих с использованием стандартного программного обеспечения / Ю. А. Мощинский., А. П. Петров // Электричество. 2001. № 7. С. 43–48.

7. Бешта, А. С. Определение параметров схемы замещения асинхронного двигателя при несимметричном питании статоров / А. С. Бешта, А. А. Семин // Электромеханические и энергосберегающие системы. 2014. Вып. 2. С. 10–16.

8. Беспалов, В. Я. Математическая модель асинхронного двигателя в обобщенной ортогональной системе координат / В. Я. Беспалов, Ю. А. Мощинский, А. П. Петров // Электричество. 2002. № 8. С. 33–39.

9. Беспалов, В. Я. Динамические показатели трехфазных асинхронных двигателей, включаемых в однофазную сеть / В. Я. Беспалов, Ю. А. Мощинский, А. П. Петров // Электротехника. 2000. № 1. С. 13–19.

10. Шуруб, Ю. В. Математическая модель асинхронного конденсаторного двигателя с тиристорным управлением / Ю. В. Шуруб // Техническая электродинамика. 1999. № 4. С. 52–56.

11. Лесник, В. А. Учет дифференциальных параметров при математическом моделировании несимметричных режимов работы асинхронных генераторов / В. А. Лесник, Ю. В. Шуруб // Техническая электродинамика. 2003. № 1. С. 45–48.

12. Rogers, G. An Induction Motor MOdel with Deep-Bar Effect and Learage Inductance Saturation / G. Rogers, D. Beraraghana // Arhiv fur Electrotechnik. 1978. Vol. 60, No 4. P. 193–201.

13. Stakhiv, P. Influence of Saturation and Skin Effect on Current Harmonic Spectrum of Asynchronous Motor Powered by Thyristor Voltage Regulator / P. Stakhiv, A. Malyar // Proceedings of the IVth International Workshop Computational Problems of Electrical Engineering, Gdynia, Poland, June 1–3, 2005. Gdynia, 2005. P. 58–60.

14. Фильц, Р. В. Алгоритм расчета переходных процессов в асинхронной машине с учетом насыщения и вытеснения тока / Р. В. Фильц, Е. А. Онышко, Е. Г. Плахтына // Преобразователи частоты для электропривода. Кишинев: Штиинца, 1979. С. 11–22.

15. Mathematical Modeling of Processes in Asynchronous Motors with Capacitors Connected in Series / V. Malyar [et al.] // 16th International Conference on Computational Problems of Electrical Engineering (CPEE 2015). Lviv, 2015. P. 107–109.

16. Копылов, И. П. Об уравнениях асинхронной машины в различных системах координат / И. П. Копылов, Р. В. Фильц, Я. Я. Яворский // Известия вузов СССР. Электромеханика. 1986. № 3. С. 22–33.

17. Фильц, Р. В. Математические основы теории электромеханических преобразователей / Р. В. Фильц. Киев: Наукова думка, 1979. 208 с.

18. Маляр, В. С. Математическое моделирование периодических режимов работы электротехнических устройств / В. С. Маляр, А. В. Маляр // Электронное моделирование. 2005. Т. 27, № 3. С. 39–53.

19. Яковлев, М. Н. К решению систем нелинейных уравнений методом дифференцирования по параметру / М. Н. Яковлев // Журнал вычислительной математики и математической физики. 1964. Т. 4, № 1. С. 146–149.

Для цитирования:

Маляр В.С., Маляр А.В. УСТАНОВИВШИЕСЯ РЕЖИМЫ И СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТРЕХФАЗНОГО АСИНХРОННОГО ДВИГАТЕЛЯ ПРИ ПИТАНИИ ОТ ОДНОФАЗНОЙ СЕТИ. Энергетика. Известия высших учебных заведений и энергетических объединений СНГ. 2016;59(6):536-548. https://doi.org/10.21122/1029-7448-2016-59-6-536-548

For citation:

Malyar V.S., Malyar V.V. ESTABLISHED MODES AND STATIC CHARACTERISTICS OF THREE-PHASE ASYNCHRONOUS MOTOR POWERED WITH SINGLE PHASE NETWORK. ENERGETIKA. Proceedings of CIS higher education institutions and power engineering associations. 2016;59(6):536-548. (In Russ.) https://doi.org/10.21122/1029-7448-2016-59-6-536-548

Контент доступен под лицензией Creative Commons Attribution 4.0 License.