Как проверить двигатель на перегрузочную способность

Как проверить двигатель на перегрузочную способность

Выбрав двигатель подходящей мощности и нужных оборотов по каталогу производителя, убедившись, что значения его номинальных напряжения и тока соответствуют вашей сети, подобрав тип крепления и условия вентиляции именно для вашего оборудования, убедившись, что исполнение корпуса подходит для условий окружающей среды, — двигатель необходимо проверить. И проверяют двигатель не просто на работоспособность, а на перегрузку, на нагрев, на условия пуска в установленном виде.

Поверка на нагрев

Для проверки двигателя на нагрев применяют методы эквивалентного тока, эквивалентной мощности, эквивалентного момента.

Проверку по методу эквивалентного тока применяют тогда, когда имеется точный, заранее полученный, график зависимости тока от времени в процессе работы двигателя. Такой график получается экспериментальным или расчетным путем. И если двигатель по результатам проверки удовлетворяет условию:

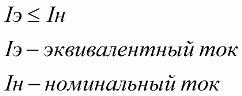
то проверку по нагреву он проходит.

Проверка по методу эквивалентного момента подойдет тем двигателям, которые работают при постоянном магнитном потоке. К таким двигателям относятся: двигатели постоянного тока с независимым возбуждением и асинхронные двигатели, работающие при скольжении близком к номинальному. Двигатель пройдет проверку на нагрев, если будет выполнено условие:

Проверку по методу эквивалентной мощности применяют лишь для тех двигателей, работа которых предполагается не только при постоянном магнитном потоке, но и при постоянных оборотах. Данные условия соблюдаются тогда, когда двигатель работает под переменной нагрузкой меньше номинальной при почти постоянных оборотах. Условие проверки следующее:

Когда двигатель работает повторно кратковременно, то эквивалентный ток, эквивалентный момент и эквивалентная мощность берутся исключительно в рабочие промежутки времени, паузы исключаются из рассмотрения. Если теоретические значения продолжительностей включения (ПВ) отличаются от стандартных, то эквивалентное значение продолжительности включения приводится к стандартному значению ПВ вот так:

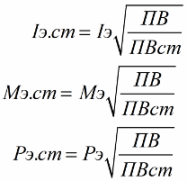
Проверка считается успешной, если двигатель удовлетворяет условиям нагрева при заданном ПВст:

Если эквивалентные мощность, момент или ток, превысят номинал данного двигателя, то перегрев будет недопустимым, а значит необходимо будет выбрать двигатель большей номинальной мощности, после чего повторить проверку на перегрев с учетом реальных ПВ.

Проверка на перегрузку

Исходя из известной нагрузочной диаграммы (зависимость момента на валу от времени), проверяют двигатель на перегрузку по следующим условиям:

Проверку по условиям пуска выполняют исходя из следующих условий:

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Ранее на эту тему: Электропривод

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Проектирование главного привода

Выбор электродвигателя и маховика. В основе существующих методик расчета мощности двигателя и момента инерции маховика лежит метод эквивалентного тока. Однако в связи с трудностью его прямой реализации при традиционных методах расчета применяют косвенные способы оценки нагрева двигателя главного привода, например по неравномерности вращения двигателя. Математическое моделирование позволяет отказаться от косвенных способов такой оценки и решать задачу выбора мощности двигателя и момента инерции маховика на основе прямого применения метода эквивалентного тока.

Выбор электродвигателя и маховика рассмотрим на примере листоштампо-вочного пресса двойного действия К460 (см. рис. 24.16) с асинхронным двигателем главного привода 4А132S4УЗ (7,5 кВт, 1440 об/мин.) и моментом инерции маховика 47 кг м2 с использованием математической модели (см. рис. 24.15). Для решения задачи в модели пресса должны быть представлены двигатель главного привода, маховик, технологическая нагрузка. Кроме того, для полноценного учета затрат энергии при работе пресса в модель следует включить все элементы, которые являются источниками или причиной этих затрат: элементы, при работе которых возникают силы трения (подшипники, шарниры, направляющие, зубчатые и фрикционные передачи, фрикционные муфты и тормоза и пр.), упругие элементы, преобразователи входной энергии. В модели пресса (см. рис. 24.14) из упомянутых элементов имеются: двигатель главного привода /; маховик 3; клиноременная передача 2; муфта с элементами фрикционных пар 25, 26, 28, 30 и шлицевых соединений 27, 29; пневмоцилиндр 31; тормоз 34; быстроходная зубчатая передача 4; тихоходная зубчатая передача 5; подшипники и шарниры 21, 24 и др.; направляющие вытяжного 22 и прижимного 23 ползунов; технологическая сила (см. табл. 24.6).

При моделировании работы пресса на каждом шаге интегрирования вычисляется момент двигателя привода. В модели DVА с учетом этого момента вычисляются частота вращения ротора; скольжение; активный, реактивный и полный фазные токи; эквивалентный и номинальный токи. Эквивалентный ток определяется в процессе моделирования по итогам выполненной части и является переменной величиной. Следует принимать во внимание значение эквивалентного тока в конце любого установившегося цикла работы пресса. При равенстве эквивалентного тока в конце цикла номинальному току двигателя его режим работы будет соответствовать номинальному, при меньшем значении эквивалентного тока двигатель будет недогружен, а при большем -перегружен. Недогрузка и перегрузка двигателя ухудшают экономические показатели работы кривошипного пресса. Для исключения влияния нестационарного периода работы пресса, например периода разгона маховика, вычисление эквивалентного тока начинается в фиксированный момент модельного времени, который вводится как один из параметров модели DVА. Его значение можно принимать равным времени начала первого цикла работы пресса. Эквивалентный и номинальный токи вычисляются как расчетные переменные и выводятся с помощью универсальных индикаторов. График номинального тока представляет собой прямую линию, поскольку он является параметром двигателя и, следовательно, представляет собой константу. Вывод графика номинального тока создает удобство для сопоставления с ним эквивалентного тока.

Для определения мощности двигателя и момента инерции маховика при заданном графике технологической силы и времени цикла следует при предварительно назначенных значениях мощности двигателя и момента инерции маховика выполнить моделирование и сопоставить значения эквивалентного тока в конце

любого цикла работы пресса с номинальным. При превышении эквивалентным током номинального (двигатель перегружен) следует назначить типоразмер двигателя большей мощности или увеличить момент инерции маховика. В противном случае (двигатель недогружен) необходимо выбрать типоразмер двигателя меньшей мощности или уменьшить момент инерции маховика. Увеличение момента инерции маховика приводит к меньшим отклонениям частоты вращения двигателя от номинальной, при которых КПД и коэффициент мощности двигателя максимальны. Таким образом, уменьшение нагрузки двигателя при увеличении момента инерции имеет место за счет повышения КПД и коэффициента мощности двигателя. Однако такое изменение нагрузки двигателя при варьировании моментом инерции маховика не может быть значительным. Поэтому при большой разнице эквивалентного и номинального токов (15. 30 % и выше) следует изменять мощность двигателя, а при небольшой — момент инерции маховика. Окончание процесса подбора мощности двигателя и момента инерции маховика определяется достижением требуемой точности совпадения эквивалентного и номинального токов. Подбор момента инерции маховика может быть ускорен применением интерполяции и экстраполяции данных, полученных на предыдущих шагах.

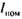токов — равной 0,1 %.

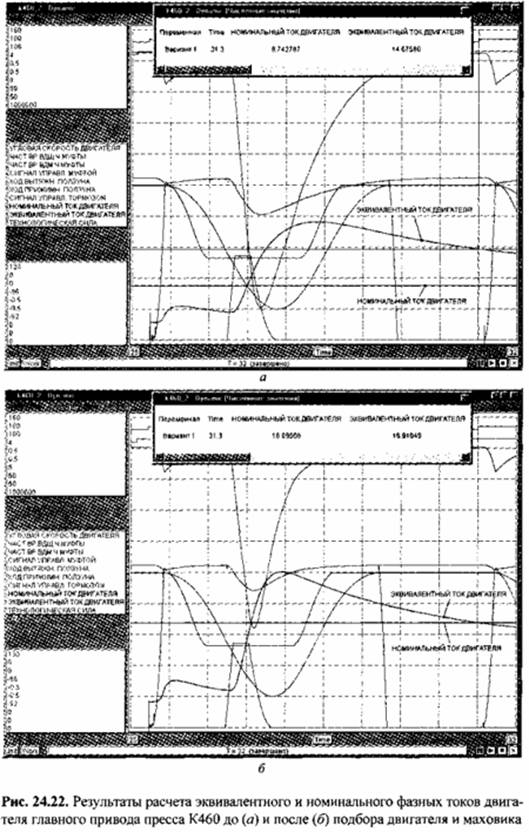
Согласно полученным результатам, при этих условиях эквивалентный ток в конце цикла больше номинального на 67,9 %, тогда как после подбора двигателя и маховика — на 0,059 % (рис. 24.22, б).

Для принятых условий номинальная нагрузка двигателя имеет место при мощности двигателя 15 кВт и моменте инерции маховика 52,21 кгм2.

Расчет баланса энергозатрат и КПД пресса. В моделях элементов, обладающих диссипативными свойствами, вычисляются входная и выходная энергии и (или) ее потери при работе элемента, а в моделях элементов, обладающих способностью накапливать энергию, — накопленная энергия. Значения входной, выходной и накопленной энергии, а также ее потери определяются в процессе моделирования по итогам выполненной части и сами являются переменными величинами. Вычисленные величины могут быть выведены как расчетные переменные с помощью универсальных индикаторов. Их значения имеют характер нарастающего итога в течение моделирования. При определении потерь энергии их следует относить к одному циклу работы пресса, т. е. находить разницу выводимых величин для начала и конца выбранного цикла.

При моделировании работы пресса при различных следующих одна за другой операциях (многопереходная штамповка) определение потерь энергии следует относить к составному циклу работы пресса. Баланс затрат энергии приведен в табл. 24.7.

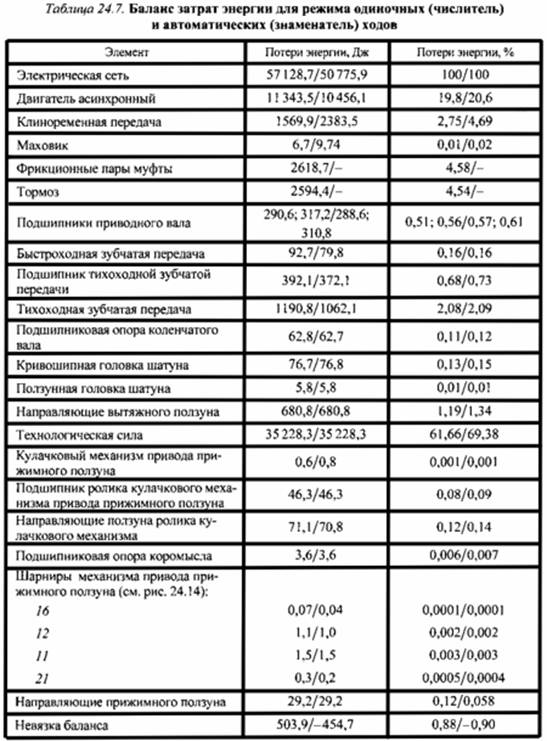
Анализ полученных результатов позволяет сделать следующие выводы.

КПД пресса составляет 61,66% для режима одиночных ходов и 69,38 % для режима автоматических ходов.

Близость к нулю потерь (накопления) энергии маховика в цикле означает, что режим работы привода пресса в цикле установившийся.

Наибольшие потери энергии имеют место в электродвигателе и составляют 19,8 и 20,6% для режима одиночных и автоматических ходов соответственно.

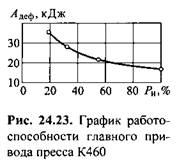
График работоспособности кривошипного пресса. Моделирование работы кривошипного пресса позволяет решать задачу определения времени цикла для операций различной энергоемкости из условия номинальной нагрузки двигателя главного привода. Однако предварительно должна быть выбрана мощность двигателя и момент инерции маховика.

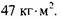Энергоемкость операции изменяли пропорциональным уменьшением значений силы и перемещения на графике нагружения.

Таблица 24.8. Продолжительность цикла и коэффициент использования ходов пресса модели К460 для операций различной энергоемкости

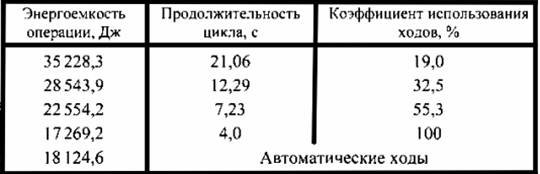
При выполнении энергетических расчетов кривошипных прессов путем математического моделирования учитываются все энергозатраты, имеющие место в представленных в модели элементах пресса; потери энергии, связанные с упругим деформированием элементов, например станины, с разгоном и торможением маховых масс; достоверно определяется КПД пресса. Учет энергозатрат осуществляется как при рабочем ходе, так и во время холостых ходов и пауз в работе пресса.

Энергетические расчеты могут быть выполнены и для составных циклов, например при многооперационной штамповке. Изложенные подходы остаются в силе и в случае оснащения пресса вспомогательными устройствами, приводимыми от двигателя главного привода, например подачами; а для кривошипных автоматов любой сложности — при условии достаточной полноты их представления в математической модели.

Проверка двигателей по нагреву в продолжительном режиме

Если известна нагрузочная диаграмма двигателя и его тепловые параметры, то можно построить график t (t) и, оценив действительный перегрев, сравнить его с допустимым. Этот путь весьма громоздок, в связи с чем на практике пользуются упрощенными приемами, основанными на косвенной оценке перегрева. В основе этих приемов лежит метод средних потерь .

Пусть нагрузочная диаграмма двигателя имеет циклический характер, а момент в каждом цикле не остается неизменным, т.е. двигатель работает с переменной нагрузкой (режимы S6 , S7 или S8 ).

Рассмотрим “далекий” цикл, в котором тепловые процессы в двигателе установились, т.е. температуры перегрева в начале и в конце цикла равны, а в течение цикла t изменяется около среднего уровня t ср . Равенство температур перегрева в начале и конце цикла свидетельствует о том, что количество тепла, запасенное в двигателе к началу цикла, не отличается от количества тепла, запасенного в двигателе в конце цикла, т.е. тепло в двигателе не запасается. Это значит, что все выделившееся за цикл тепло отводится в окружающую среду., т.е.

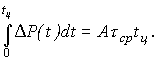(11)

Уравнение (11), выражающее закон сохранения энергии в интегральной форме, можно записать в следующем виде:

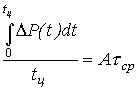
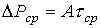, (12)

т.е. средняя за цикл мощность потерь пропорциональна средней температуре перегрева .

Для номинального режима, в соответствии с (6) имеем:

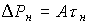, (13)

где D Р н – номинальная мощность потерь;

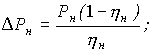
Р н – номинальная мощность двигателя;

h н – номинальный КПД двигателя;

t н = t доп — номинальная (допустимая) температура перегрева двигателя.

Сравнивая (12) и (13), легко прийти к формулировке метода средних потерь: если средняя за цикл мощность потерь не превосходит номинальную мощность потерь , т.е.

,

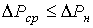то средняя температура перегрева не превышает допустимую

.

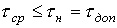Пусть нагрузочная диаграмма, построенная для предварительно выбранного двигателя, имеет вид, представленный на рис. 9. Для каждого уровня нагрузки двигателя (на каждом участке диаграммы) вычислим мощность P i = M i w i по кривой h ( Р/Р н ) определим значение КПД h i , и найдем потери

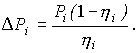
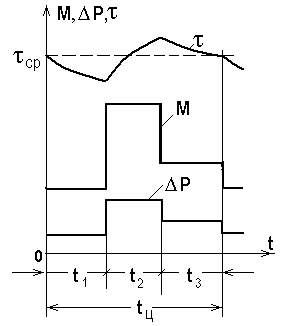
Рис. 9. Нагрузочная диаграмма и кривая t (t) для “далекого” цикла

Затем вычислим средние потери:

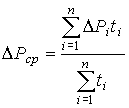
(в примере n = 3) и сравним их с D Р н . Если D Р ср Ј D Р н , двигатель выбран правильно.

Если при сопоставлении средних потерь за цикл с номинальными потерями окажется, что D Р ср > D Р н , то двигатель будет перегреваться, что недопустимо. Наоборот, при D Р ср D Р н двигатель будет плохо использован по нагреву. В обоих случаях необходимо выбрать другой двигатель, перестроить нагрузочную диаграмму и вновь проверить двигатель по нагреву путем сопоставления средних потерь при переменном графике нагрузки с номинальными потерями при постоянной нагрузке.

Метод средних потерь позволяет оценивать среднюю температуру перегрева, не прибегая к построению t (t) . Действительная температура отличается от средней, однако, если выполняется условие

то эта разница будет весьма малой. Условие (14) является необходимым при использовании метода средних потерь .

Метод средних потерь требует знания кривой КПД двигателя в функции его нагрузки и предварительного определения потерь на каждом из участков графика, что вносит некоторые усложнения в расчет. Если в распоряжении расчетчика в результате построения нагрузочной диаграммы имеются кривые тока в функции времени, то при некоторых условиях можно произвести проверку двигателя по нагреву без вычисления потерь, воспользовавшись методом эквивалентного тока .

В соответствии с (6.8) потери в двигателе можно рассматривать как сумму постоянных потерь k , не зависящих от нагрузки, и переменных I 2 R , всецело определяемых нагрузкой.

Назовем эквивалентным током такой неизменяющийся ток, при работе с которым в электрическом двигателе выделяются потери, равные средним потерям при переменном графике нагрузки, т.е.

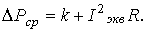(15)

Средняя мощность потерь за цикл при переменном графике нагрузки двигателя и продолжительном режиме работы

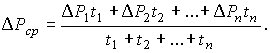
Выразив потери на каждом из участков графика D Р i через постоянную и переменную составляющие и заменив средние потери их значением через эквивалентный ток, получим :

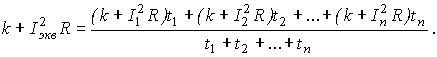
Открыв скобки и сгруппировав постоянные и переменные потери, получим:

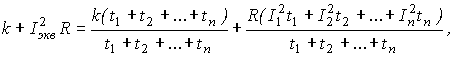
откуда эквивалентный ток при переменном графике нагрузки

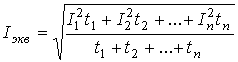(16)

или в общем случае

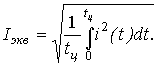(17)

Вычисленный таким образом эквивалентный ток сопоставляется с номинальным током предварительно выбранного двигателя и если окажется, что I экв Ј I н , то двигатель удовлетворяет требованиям нагрева.

Метод эквивалентного тока, как и метод средних потерь, основан на допущении близости среднего за цикл и максимального перегревов. Это допущение не влечет за собой существенной погрешности, если выполнено условие (14). Кроме того, метод эквивалентного тока исходит из предположения независимости потерь в стали и механических от нагрузки и предполагает постоянство величины сопротивления главной цепи двигателя на всех участках заданного графика нагрузки. Следовательно, в случаях, когда k № const (например, когда асинхронный двигатель работает при изменяющемся напряжении) или R № const (асинхронный двигатель с глубоким пазом или двойной клеткой в режиме переменного скольжения), метод эквивалентного тока может привести к существенным погрешностям.

В ряде случаев при проверке двигателя по нагреву удобно пользоваться графиком момента, развиваемого двигателем, в функции времени. Если поток двигателя при этом постоянен, то между моментом и током существует прямая пропорциональность (М = сI) . В этих случаях возможна проверка двигателя по эквивалентному моменту, который для ступенчатого графика вычисляется по формуле

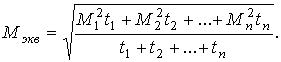(18)

Величина эквивалентного момента сопоставляется с номинальным моментом, и если М экв Ј М н , то двигатель удовлетворяет требованиям нагрева.

Метод эквивалентного момента применим для проверки по нагреву синхронных и асинхронных двигателей нормального исполнения и двигателей независимого возбуждения при работе с номинальным потоком.

Если нагрузочная диаграмма двигателя задана в виде графика мощности, то проверка двигателя по нагреву на основе заданного графика может быть произведена непосредственно лишь в случаях, когда между мощностью и током существует прямая пропорциональность, что имеет место при работе двигателя с постоянным потоком и скоростью.

Для ступенчатого графика эквивалентная мощность вычисляется по формуле

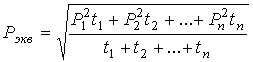(19)

и сравнивается с номинальной мощностью двигателя; проверяется выполнение условия Р экв Ј Р н .

200 тыс км/с в стекле и

3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью «Температура эфира и красные смещения»), разную скорость для разных частот (см. статью «О скорости ЭМ-волн»)
2. В релятивизме «свет» есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский «свет» — это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те «подтверждающие теорию Эйнштейна факты», которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.

Методы эквивалентного момента и мощности.

Дата добавления: 2015-09-15 ; просмотров: 6045 ; Нарушение авторских прав

Часто для проверки двигателя по нагреву и особенно при предварительном его выборе приходится пользоваться графиками момента или мощности, развиваемых двигателем.

При неизменном магнитном потоке, когда момент двигателя M=cI, можно для проверки двигателя воспользоваться методом эквивалентного момента.

Для ступенчатого графика эквивалентный момент определяем по формуле

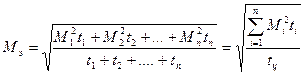(1)

При изменяющейся теплоотдаче вместо t_ц в (1) подставляем 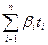. Эквивалентный момент сопоставляем с номинальным моментом двигателя, и если 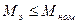, то двигатель полностью используется по нагреву.

Этот метод применим для двигателей постоянного тока с независимым возбуждением, а также асинхронных и синхронных двигателей, работающих с номинальным магнитным потоком. Кроме того, для применения и этого метода должно выполняться условие неизменности постоянных потерь и активных сопротивлений двигателя.

Когда нагрузочная диаграмма электропривода и механизма задана графиком мощности, развиваемой двигателем, выбор и проверка его по нагреву могут быть произведены методом эквивалентной мощности, но лишь в том случае, если между мощностью и током существует прямая пропорциональность, т. е. при ΔР_С = const, R=const, Ф = const, ω = const = ω_ном.

Эквивалентную мощность для ступенчатого графика оп­ределяем по формуле

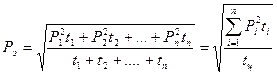
и сравниваем с номинальной мощностью двигателя, при этом должно быть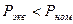

Метод эквивалентной мощности может быть применен для проверки по нагреву асинхронных и синхронных двигателей, а также двигателей постоянного тока независимого- возбуждения, работающих с номинальным потоком и постоянной или мало меняющейся угловой скоростью.

Методом эквивалентной мощности можно воспользоваться и в случае переменной угловой скорости, если привести мощность при угловой скорости ω_i к эквивалентной мощности при ω=ω_о, используя соотношение

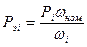. Тогда формула эквивалентной мощности для случая переменных угловой скорости и теплоотдачи примет вид:

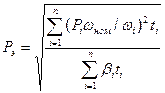
Замечание по данной главе.

Следует отметить, что нее рассмотренные методы проверки двигателя по нагреву при перемонной нагрузке представляют собой методы эквивалентного преобразования нагрузочной диаграммы к стандартной диаграмме для режима S1, на который рассчитан двигатель продолжительного режима. Этими методами (при выполнении соответствующих ограничений) могут быть проверены двигатели продолжительного режима, работающие в режимах S7, S8 и подобных им и в режимах S3, S4, S5. Наиболее универсальным и точным из всех рассмотренных методов является метод средних или эквивалентных потерь.

Если методы средних потерь и эквивалентного тока пригодны только для проверки но нагреву предварительно выбранного двигателя, то методами эквивалентного момента и мощности можно воспользоваться для предварительного выбора двигателя по нагрузочной диаграмме механизма (или по упрощенной нагрузочной диаграмме двигателя, построенной без учета момента инерции двигателя), считая, что момент (мощность) двигателя равен соответствующим статическим значениям. Такой выбор является более точным, чем выбор по средней мощности. Предварительный выбор производят по формулам: