Термодинамические циклы

Термодинамические циклы

Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура и энтропия).

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу.

Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела).

Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, цикл Стирлинга и цикл Эрикссона ( англ. ) ), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора. Общим (т.е. указанные циклы частный случай) для всех этих циклов с регенерацией является Цикл Рейтлингера. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью.

Содержание

• 1 Основные принципы
• 2 Вычисление работы и КПД в термодинамическом цикле
• 3 Цикл Карно и максимальный КПД тепловой машины
• 4 См. также
• 5 Ссылки
• 6 Литература

Основные принципы [ править | править код ]

Прямое преобразование тепловой энергии в работу запрещается постулатом Томсона (см. Второе начало термодинамики). Поэтому для этой цели используются термодинамические циклы.

Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты ( Q 1 > ) у нагревателя и отдаёт количество теплоты Q 2 > холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом,

A = ( Q 1 − Q 2 ) − Δ U = Q 1 − Q 2 -Q_<2>)-Delta U=Q_<1>-Q_<2>> ,

так как изменение внутренней энергии U в круговом процессе равно нулю (это функция состояния).

Напомним, что работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю.

При этом нагреватель потратил энергию Q 1 > . Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен

η = A Q 1 = Q 1 − Q 2 Q 1 >>=-Q_<2>>>>> .

Вычисление работы и КПД в термодинамическом цикле [ править | править код ]

Работа в термодинамическом цикле, по определению, равна

A = ∮ C P d V PdV> ,

где C — контур цикла.

C другой стороны, в соответствии с первым началом термодинамики, можно записать

A = ∮ C δ Q − d U = ∮ C δ Q = ∮ C T d S delta Q-dU=oint _delta Q=oint _TdS> .

Аналогичным образом, количество теплоты, переданное нагревателем рабочему телу, равно

Q 1 = ∫ A → B δ Q = ∫ A → B T d S =int _delta Q=int _TdS> .

Отсюда видно, что наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия.

Цикл Карно и максимальный КПД тепловой машины [ править | править код ]

Основная статья: Цикл Карно.

Представим себе следующий цикл:

Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу Q 1 = T H ( S 2 − S 1 ) =T_(S_<2>-S_<1>)> тепла в изотермическом процессе (при постоянной температуре), при этом объём рабочего тела увеличивается.

Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически (без теплообмена с окружающей средой). При этом его температура уменьшается до температуры холодильника.

Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему Q 2 = T X ( S 2 − S 1 ) =T_(S_<2>-S_<1>)> тепла в изотермическом процессе. При этом объём рабочего тела уменьшается.

Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя.

Его КПД равен, таким образом,

η = Q 1 − Q 2 Q 1 = T H ( S 2 − S 1 ) − T X ( S 2 − S 1 ) T H ( S 2 − S 1 ) = T H − T X T H -Q_<2>>>>=(S_<2>-S_<1>)-T_(S_<2>-S_<1>)>(S_<2>-S_<1>)>>=-T_>>>> ,

то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.

Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД.

Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.

II. Молекулярная физика

Тестирование онлайн

Тепловой двигатель

Двигатель, в котором происходит превращение внутренней энергии топлива, которое сгорает, в механическую работу.

Любой тепловой двигатель состоит из трех основных частей: нагревателя, рабочего тела (газ, жидкость и др.) и холодильника. В основе работы двигателя лежит циклический процесс (это процесс, в результате которого система возвращается в исходное состояние).

Прямой цикл теплового двигателя

Общее свойство всех циклических (или круговых) процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ (происходит расширение) и отдает холодильнику количество теплоты Q₂, когда возвращается в исходное состояние и сжимается. Полное количество теплоты Q=Q₁-Q₂, полученное рабочим телом за цикл, равно работе, которую выполняет рабочее тело за один цикл.

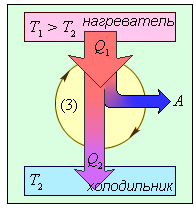
Обратный цикл холодильной машины

При обратном цикле расширение происходит при меньшем давлении, а сжатие — при большем. Поэтому работа сжатия больше, чем работа расширения, работу выполняет не рабочее тело, а внешние силы. Эта работа превращается в теплоту. Таким образом, в холодильной машине рабочее тело забирает от холодильника некоторое количество теплоты Q₁ и передает нагревателю большее количество теплоты Q₂.

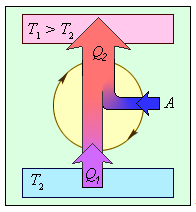
Коэффициент полезного действия

Прямой цикл:

Показатель эффективности холодильной машины:

Цикл Карно

В тепловых двигателях стремятся достигнуть наиболее полного превращения тепловой энергии в механическую. Максимальное КПД.

На рисунке изображены циклы, используемые в бензиновом карбюраторном двигателе и в дизельном двигателе. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30%, у дизельного двигателя – порядка 40 %.

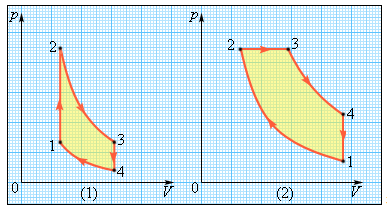
Французский физик С.Карно разработал работу идеального теплового двигателя. Рабочую часть двигателя Карно можно представить себе в виде поршня в заполненном газом цилиндре. Поскольку двигатель Карно — машина чисто теоретическая, то есть идеальная, силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю. Механическая работа максимальна, если рабочее тело выполняет цикл, состоящий из двух изотерм и двух адиабат. Этот цикл называют циклом Карно.

участок 1-2: газ получает от нагревателя количество теплоты Q₁ и изотермически расширяется при температуре T₁
участок 2-3: газ адиабатически расширяется, температура снижается до температуры холодильника T₂
участок 3-4: газ экзотермически сжимается, при этом он отдает холодильнику количество теплоты Q₂
участок 4-1: газ сжимается адиабатически до тех пор, пока его температура не повысится до T₁.
Работа, которую выполняет рабочее тело — площадь полученной фигуры 1234.

Функционирует такой двигатель следующим образом:

1. Сначала цилиндр вступает в контакт с горячим резервуаром, и идеальный газ расширяется при постоянной температуре. На этой фазе газ получает от горячего резервуара некое количество тепла.
2. Затем цилиндр окружается идеальной теплоизоляцией, за счет чего количество тепла, имеющееся у газа, сохраняется, и газ продолжает расширяться, пока его температура не упадет до температуры холодного теплового резервуара.
3. На третьей фазе теплоизоляция снимается, и газ в цилиндре, будучи в контакте с холодным резервуаром, сжимается, отдавая при этом часть тепла холодному резервуару.
4. Когда сжатие достигает определенной точки, цилиндр снова окружается теплоизоляцией, и газ сжимается за счет поднятия поршня до тех пор, пока его температура не сравняется с температурой горячего резервуара. После этого теплоизоляция удаляется и цикл повторяется вновь с первой фазы.

КПД цикла Карно не зависит от вида рабочего тела

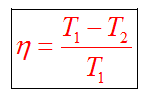
для холодильной машины

В реальных тепловых двигателях нельзя создать условия, при которых их рабочий цикл был бы циклом Карно. Так как процессы в них происходят быстрее, чем это необходимо для изотермического процесса, и в то же время не настолько быстрые, чтоб быть адиабатическими.

5.6. Двигатель внутреннего сгорания

Тепловой двигатель — это периодически действующее устройство, в котором тепловая энергия преобразуется в механическую работу.

Тепловые двигатели разнообразны по конструкции и назначению. К ним относятся паровые машины, двигатели внутреннего сгорания, реактивные двигатели и т. д. (см. рис. 5.9).

Рис. 5.9. Тепловые двигатели: 1 — паровая машина; 2 — двигатель внутреннего сгорания; 3 — газовая турбина; 4 — ракетный двигатель

Несмотря на многообразие, в основе практически всех тепловых двигателей лежит общий принцип — принцип циклического действия. Основными частями любого теплового двигателя являются: нагреватель, рабочее тело и холодильник.

Рассмотрим в качестве примера работу четырехтактного двигателя внутреннего сгорания. В этом двигателе высокая температура достигается за счет сгорания рабочей смеси (бензина с воздухом) внутри цилиндра двигателя; воспламенение смеси происходит с помощью искрового зажигания. Перечислим основные стадии работы четырехтактного двигателя внутреннего сгорания:

Работа четырехтактного двигателя внутреннего сгорания показана на рис. 5.10.

Рис. 5.10. Работа четырехтактного двигателя внутреннего сгорания

Рассмотрим идеализированный процесс (цикл Отто), близкий к используемому в четырехтактном двигателе внутреннего сгорания. Цикл Отто изображен на рис. 5.11.

Рис. 5.11. Идеализированный цикл четырехтактного двигателя внутреннего сгорания (цикл Отто)

Как обычно, термодинамические параметры имеют индексом номер соответствующей точки на рисунке (в данном случае надо будет помнить, что V₃ = V₂; V₄ = V₁).

Изобара А—1. Первый такт цикла. Вследствие движения поршня в цилиндр всасывается горючее. Приближенно можно считать, что это происходит при атмосферном давлении p₁. Объем увеличивается от V₁ до V₂.

Адиабата 1—2. Второй такт цикла. Теплообмена со средой нет. Поршень движется в обратном направлении, адиабатно сжимая смесь от объема V₁ до объема V₂. При этом повышается давление, и температура растет от Т₁ до Т₂. Связь температур и объемов в начале и конце адиабатной части цикла дается соотношением

Изохора 2—3. Начало третьего такта. Под действием электрической искры горючая смесь взрывается: давление почти мгновенно возрастает до значения р₃, а объем еще не успевает измениться. Температура растет от T₂ до Т₃ за счет тепла, выделенного при взрыве. Работа не производится, а количество полученного тепла выражается формулой

Адиабата 3—4. Продолжение третьего такта. Теплообмена со средой нет. Газ адиабатно расширяется до максимального объема цилиндра V₁, падают температура и давление. Связь температур и объемов в начале и конце адиабаты дается уравнением

Изохора 4—l. Конец третьего такта. Открывается клапан, давление падает до атмосферного при постоянном объеме. Температура также падает до значения Т₁.

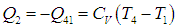
Изобара 1—А. Четвертый такт. Поршень выталкивает из цилиндра отработанные газы, система возвращается в начальное состояние. Поскольку участок А-1 проходится дважды в разных направлениях, соответствующие вклады в работу и в теплоту сокращаются и могут не приниматься во внимание.

Таким образом, получаем для КПД цикла

Из уравнений (1), (3) следует равенство отношений

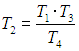
Подставляя (6) в (5), приходим к окончательному выражению для КПД цикла

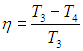
Оно получилось очень похожим на формулу для КПД цикла Карно, но обратим внимание, что максимальной температурой здесь является температура в точке 3 (Т_mах = Т₃), а минимальной — температура в точке 1 (T_min = T₁). Поэтому КПД цикла Карно, работающего между такими температурами, равнялся бы

Разность этих двух выражений отлична от нуля:

поскольку Т₄ > T₁. Мы воочию убедились, что КПД рассмотренного цикла меньше КПД цикла Карно. Заметим также, что КПД цикла Отто можно выразить через отношение объемов:

Величина V₁/V₂ называется сжатием. Получается, что КПД рассмотренного цикла определяется только величиной сжатия горючей смеси и показателем адиабаты.

Термодинамические циклы

Термодинамические циклы
Статья является частью серии «Термодинамика».
Цикл Аткинсона
Цикл Брайтона/Джоуля
Цикл Гирна
Цикл Дизеля
Цикл Калины
Цикл Карно
Цикл Ленуара
Цикл Миллера
Цикл Отто
Цикл Ренкина
Цикл Стирлинга
Цикл Тринклера
Цикл Хамфри
Цикл Эрикссона
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править
См. также «Физический портал»

Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия), совпадают.

Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу.

Компонентами любой тепловой машины являются рабочее тело, нагреватель и холодильник (с помощью которых меняется состояние рабочего тела).

Обратимым называют цикл, который можно провести как в прямом, так и в обратном направлении в замкнутой системе. Суммарная энтропия системы при прохождении такого цикла не меняется. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, цикл Стирлинга и цикл Эрикссона), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора. Общим (т.е. указанные циклы частный случай) для всех этих циклов с регенерацией является Цикл Рейтлингера. Можно показать (см. статью Цикл Карно), что обратимые циклы обладают наибольшей эффективностью.

Содержание

Основные принципы

Прямое преобразование тепловой энергии в работу запрещается постулатом Томсона (см. Второе начало термодинамики). Поэтому для этой цели используются термодинамические циклы.

Для того, чтобы управлять состоянием рабочего тела, в тепловую машину входят нагреватель и холодильник. В каждом цикле рабочее тело забирает некоторое количество теплоты () у нагревателя и отдаёт количество теплоты холодильнику. Работа, совершённая тепловой машиной в цикле, равна, таким образом,

,

так как изменение внутренней энергии в круговом процессе равно нулю (это функция состояния).

Напомним, что работа не является функцией состояния, иначе суммарная работа за цикл также была бы равна нулю.

При этом нагреватель потратил энергию . Поэтому тепловой, или, как его ещё называют, термический или термодинамический коэффициент полезного действия тепловой машины (отношение полезной работы к затраченной тепловой энергии) равен

.

Вычисление работы и КПД в термодинамическом цикле

Работа в термодинамическом цикле, по определению, равна

,

где — контур цикла.

C другой стороны, в соответствии с первым началом термодинамики, можно записать

.

Аналогичным образом, количество теплоты, переданное нагревателем рабочему телу, равно

.

Отсюда видно, что наиболее удобными параметрами для описания состояния рабочего тела в термодинамическом цикле служат температура и энтропия.

Цикл Карно и максимальный КПД тепловой машины

Основная статья: Цикл Карно.

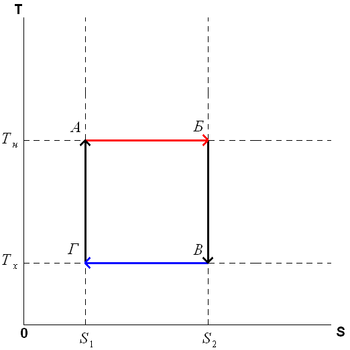
Представим себе следующий цикл:

Фаза А→Б. Рабочее тело с температурой, равной температуре нагревателя, приводится в контакт с нагревателем. Нагреватель сообщает рабочему телу тепла в изотермическом процессе (при постоянной температуре), при этом объём рабочего тела увеличивается.

Фаза Б→В. Рабочее тело отсоединяется от нагревателя и продолжает расширяться адиабатически (без теплообмена с окружающей средой). При этом его температура уменьшается до температуры холодильника.

Фаза В→Г. Рабочее тело приводится в контакт с холодильником и передает ему тепла в изотермическом процессе. При этом объём рабочего тела уменьшается.

Фаза Г→А. Рабочее тело адиабатически сжимается до исходного размера, и его температура увеличивается до температуры нагревателя.

Его КПД равен, таким образом,

,

то есть, зависит только от температур холодильника и нагревателя. Видно, что 100%-ный КПД можно получить только в том случае, если температура холодильника есть абсолютный нуль, что недостижимо.

Можно показать, что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бо́льшим КПД.

Заметим, что мощность тепловой машины Карно равна нулю, так как передача тепла в отсутствие разности температур идёт бесконечно медленно.